题目内容
14.某宾馆有50个房间供游客住宿,当每个房间的房价为每天200元时,房间会全部住满.当每个房间每天的房价每增加20元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出40元的各种费用,根据规定,每个房间每天的房价不得高于680元.设每个房间每天的房价为x(元)(x为10的正整数倍).(1)设一天订出的房间数为y,求出y与x的函数关系式及自变量x的取值范围;
(2)请你用含x的代数式表示宾馆的利润;
(3)若宾馆的利润要达到14820元,且尽量降低宾馆的成本,一天应订出多少个房间?
分析 (1)理解每个房间的房价为x元时,房价增加(x-200)元,则减少房间$\frac{x-200}{20}$间,则一天订出的房间数=一共有的房间数-房价增长减少的房间数,依此得到y与x之间的关系;
(2)每个房间订住后每间的利润是房价减去40元,每间的利润与所订的房间数的积就是利润;
(3)根据宾馆的利润要达到14820元列出方程,解方程即可.
解答 解:(1)由题意得:
y=50-$\frac{x-200}{20}$,且200≤x≤680,且x为10的正整数倍.
(2)宾馆的利润为:(x-40)(50-$\frac{x-200}{20}$)=-$\frac{1}{20}$x2+62x-2400;
(3)由题意,得-$\frac{1}{20}$x2+62x-2400=14820,
解得x1=420,x2=820,
∵尽量降低宾馆的成本,
∴x=420,此时y=50-$\frac{x-200}{20}$=39,
答:一天应订出39个房间.
点评 本题考查的是二次函数在实际生活中的应用及一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出等量关系式.

练习册系列答案
相关题目
5.某校初三学生开展毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每踢100个(含100)为优秀.下表是成绩最好的甲班和乙班各5名学生的比赛数据(单位:个)
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考.请你回答下列问题:
(1)计算两班的优秀率及比赛数据的中位数;
(2)哪一个班级学生的比赛成绩相互之间更接近,为什么?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?说明理由!
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
(1)计算两班的优秀率及比赛数据的中位数;
(2)哪一个班级学生的比赛成绩相互之间更接近,为什么?
(3)根据以上信息,你认为应该把冠军奖状发给哪一个班级?说明理由!
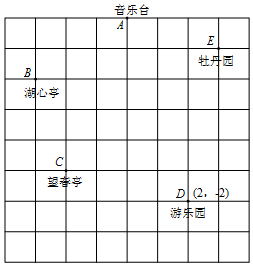 小王到公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示,可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),且一格表示一个单位长度.
小王到公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示,可是她忘记了在图中标出原点和x轴、y轴,只知道游乐园D的坐标为(2,-2),且一格表示一个单位长度.