题目内容
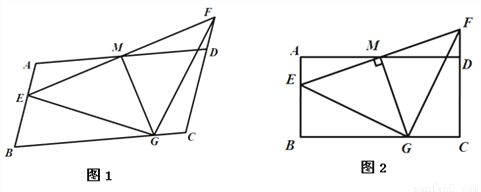
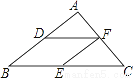
如图,在Rt△ABC中,∠ACB=90°.
(1)利用直尺和圆规按下列要求作图,并在图中标明相应的字母.(保留作图痕迹,不写作法)
①作AC的垂直平分线,交AB于点O,交AC于点D;
②以O为圆心,OA为半径作圆,交OD的延长线于点E.
(2)在(1)所作的图形中,解答下列问题.
①点B与⊙O的位置关系是_;(直接写出答案)
②若DE=2,AC=8,求⊙O的半径.
(1)画图见解析;(2)(2)①点B在⊙O上;②⊙O的半径为5. 【解析】试题分析:(1)分别以A、C为圆心,以大于线段AC一半的长度在线段AC上下两侧画弧。连接交点级为线段AC的垂直平分线,交AB于点O,交AC于点D。 (2)比较OB和OA的长,如果OA=OB则点B 在圆上,利用垂直平分线的性质,及角与角之间的等量代换,可证明OA=OB。利用勾股定理,放在∆AOD中求半径。 试...
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


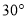 ,则这个等腰三角形的顶角度数是__________.
,则这个等腰三角形的顶角度数是__________.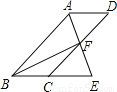
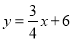 与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
与x轴、y轴分别交于点A、C两点,点B的横坐标为2.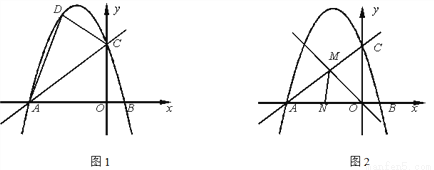
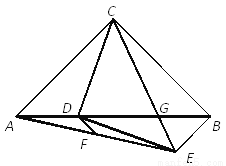
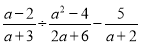 ,其中a=
,其中a=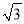 -2.
-2.