题目内容
20. 已知二次函数y=2x2-4x-6.
已知二次函数y=2x2-4x-6.(1)用配方法将y=2x2-4x-6化为y=a(x-h)2+k的形式;并写出对称轴和顶点坐标;
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)当x取何值时,y随x的增大而减少?
(4)当x取何值时,y=0,y>0,y<0;
(5)当0<x<4时,求y的取值范围.
分析 (1)直接利用配方法求出二次函数顶点坐标和对称轴得出答案;
(2)利用(1)中所求进而画出函数图象;
(3)直接利用函数图象得出增减性;
(4)利用函数图象得出y>0,y<0时对应x的取值范围;
(5)直接利用二次函数增减性以及结合极值法求出y的取值范围.
解答 解:(1)由题意可得:
y=2x2-4x-6=2(x-1)2-8,
对称轴为:直线x=1,顶点坐标为:(1,-8);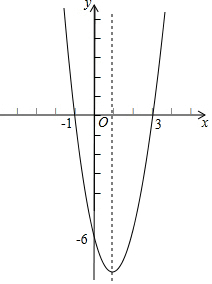
(2)如图所示:
(3)当x<1时,y随x的增大而减少;
(4)当y=0时,
则0=2x2-4x-6,
解得:x1=-1,x2=3,
当y>0时,x<-1或x>3,
当y<0时,-1<x<3;
(5)当0<x<4时,
当x=1,y=-8,当x=4,y=10
则y的取值范围为:-8≤y<10.
点评 此题主要考查了二次函数的性质以及二次函数图象、配方法求其顶点坐标,正确画出函数图象是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知等腰三角形的两边分别为a和b,且a和b满足|a-4|+(2a-b)2=0,则这个等腰三角形的周长为( )
| A. | 12 | B. | 16 | C. | 16或20 | D. | 20 |
9.阅读理解:由面积都是1的小正方格组成的方格平面叫做格点平面.而纵横两组平行线的交点叫做格点.如图1中,有9个格点,如果一个正方形的每个顶点都在格点上,那么这个正方形称为格点正方形.
(1)探索发现:按照图形完成下表:
关于格点正方形的面积S,从上述表格中你发现了什么规律?
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.

(1)探索发现:按照图形完成下表:
| 格点正方形边上格点数p | 格点正方形内格点数q | $\frac{p}{2}+q-1$ | 格点正方形面积S | |
| 图1 | 4 | 1 | 2 | 2 |
| 图2 | 4 | 4 | 5 | 5 |
| 图3 | 12 | 4 | 9 | 9 |
| 图4 | 4 | 9 | 10 | 10 |
(2)继续猜想:类比格点正方形的概念,如果一个长方形的每个顶点都在格点上,那么这个长方形称为格点长方形,对于格点长方形的面积,你认为也有类似(1)中的规律吗?试以图5中格点长方形为例来说明.

10.小刚每天从家骑自行车上学都经过三个路口,且每个路口都安装有红灯、绿灯,假如每个路口红灯和绿灯亮的时间相同,那么小刚从家出发去学校,他遇到两次红灯的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{8}$ | C. | $\frac{5}{8}$ | D. | $\frac{7}{8}$ |
 如图,已知点C在线段AB上,在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM.
如图,已知点C在线段AB上,在AB的同侧作等边三角形△ACM和△BCN,连接AN,BM. 如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M.
如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C,该抛物线的顶点为M. 如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.
如图,在△ABC中,AB=AC=8,BC=6,点D为BC上一点,BD=2.过点D作射线DE交AC于点E,使∠ADE=∠B.