题目内容
7.计算:(1)(4a3b-10b3)+(-3a2b2+10b3);
(2)(4x2y-5xy2)-(3x2y-4xy2);
(3)5a2-[a2+(5a2-2a)-2(a2-3a)];
(4)15+3(1-a)-(1-a-a2)+(1-a+a2-a3);
(5)(4a2b-3ab)+(-5a2b+2ab);
(6)(6m2-4m-3)+(2m2-4m+1);
(7)(5a2+2a-1)-4(3-8a+2a2);
(8)3x2-[5x-($\frac{1}{2}$x-3)+2x2].
分析 (1)先去括号,然后合并同类项求解;
(2)先去括号,然后合并同类项求解;
(3)先去括号,然后合并同类项求解;
(4)先去括号,然后合并同类项求解;
(5)先去括号,然后合并同类项求解;
(6)先去括号,然后合并同类项求解;
(7)先去括号,然后合并同类项求解;
(8)先去括号,然后合并同类项求解.
解答 解:(1)原式=4a3b-10b3-3a2b2+10b3
=4a3b-3a2b2;
(2)原式=4x2y-5xy2-3x2y+4xy2
=x2y-xy2;
(3)原式=5a2-a2-5a2+2a+2a2-6a
=a2-4a;
(4)原式=15+3-3a-1+a+a2+1-a+a2-a3
=-a3+2a2-3a+17;
(5)原式=4a2b-3ab-5a2b+2ab
=-a2b-ab;
(6)原式=6m2-4m-3+2m2-4m+1
=8m2-8m-2;
(7)原式=5a2+2a-1-12+24a-8a2
=-3a2+26a-13;
(8)原式=3x2-5x+$\frac{1}{2}$x-3-2x2
=x2-$\frac{9}{2}$x-3.
点评 本题考查了整式的加减,解答本题的关键是掌握去括号法则和合并同类项法则.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.二次函数y=a(x+k)2+k,无论k为何实数,其图象的顶点都在( )
| A. | 直线y=x上 | B. | 直线y=-x上 | C. | x轴上 | D. | y轴上 |
13.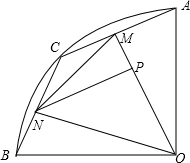 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
 如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )
如图,在半径为2的扇形AOB中,∠AOB=90°,C为弧AB上的动点,ON、OM分别与BC、AC垂直,垂足为N,M.过点N作NP⊥OM,垂足为P,则NP的长为( )| A. | 随C点的运动而变化,NP的取值范围是1≤NP≤$\sqrt{2}$ | |
| B. | 随C点的运动而变化,最大值为$\frac{3\sqrt{2}}{2}$ | |
| C. | 等于$\sqrt{2}$ | |
| D. | 随C点的运动而变化,没有最值 |
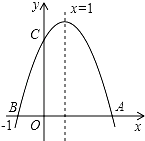 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论:
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标是(-1,0),对称轴为直线x=1,下面的四个结论: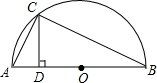 如图所示,AB是半圆O的直径,CD⊥AB,AC=5cm,BC=12cm,求CD的长.
如图所示,AB是半圆O的直径,CD⊥AB,AC=5cm,BC=12cm,求CD的长.