题目内容
6.(1)化简:$\frac{4x}{x+1}$-$\frac{4x+8}{{x}^{2}-1}$÷$\frac{x+2}{{x}^{2}-2x+1}$(2)解方程:$\frac{13}{3x-8}$=1-$\frac{4x-7}{8-3x}$.
分析 (1)原式第二项利用除法法则变形,约分后利用同分母分式的减法法则计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{4x}{x+1}$-$\frac{4(x+2)}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$=$\frac{4x}{x+1}$-$\frac{4x-4}{x+1}$=$\frac{4}{x+1}$;
(2)去分母得:12=3x-8-7+4x,
解得:x=4,
经检验x=4是分式方程的解.
点评 此题考查了解分式方程,以及分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.如果分式$\frac{x}{x-1}$没有意义,那么x的取值范围是( )
| A. | x≠0 | B. | x=0 | C. | x≠1 | D. | x=1 |
18.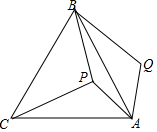 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ,若PA=6,PB=8,PC=10,则四边形APBQ的面积为( )
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ,若PA=6,PB=8,PC=10,则四边形APBQ的面积为( )
 如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ,若PA=6,PB=8,PC=10,则四边形APBQ的面积为( )
如图,P是等边三角形ABC内一点,将线段AP绕点A顺时针旋转60°得到线段AQ,连接BQ,若PA=6,PB=8,PC=10,则四边形APBQ的面积为( )| A. | 24 | B. | 12+6$\sqrt{3}$ | C. | 24+9$\sqrt{3}$ | D. | 12+9$\sqrt{3}$ |
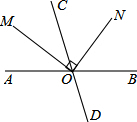 如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数.
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,且∠BON=55°,求∠BOD的度数. 如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A=110°.
如图,在平行四边形ABCD中,E为AD上一点,∠EBC=40°,且BE=BC,CE=CD,则∠A=110°.