题目内容
已知:E是线段AC上一点,AE=AB,过点E作直线EF,在EF上取一点D,使得∠EDB=∠EAB,联结AD.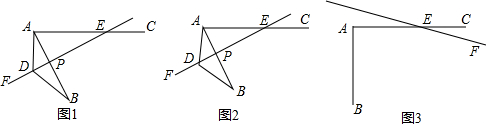
(1)若直线EF与线段AB相交于点P,当∠EAB=60°时,如图1,求证:ED=AD+BD;
(2)若直线EF与线段AB相交于点P,当∠EAB=α(0°<α<90°)时,如图2,请你直接写出线段ED、AD、BD之间的数量关系(用含α的式子表示);
(3)若直线EF与线段AB不相交,当∠EAB=90°时,如图3,请你补全图形,写出线段ED、AD、BD之间的数量关系,并证明你的结论.

(1)若直线EF与线段AB相交于点P,当∠EAB=60°时,如图1,求证:ED=AD+BD;
(2)若直线EF与线段AB相交于点P,当∠EAB=α(0°<α<90°)时,如图2,请你直接写出线段ED、AD、BD之间的数量关系(用含α的式子表示);
(3)若直线EF与线段AB不相交,当∠EAB=90°时,如图3,请你补全图形,写出线段ED、AD、BD之间的数量关系,并证明你的结论.
考点:全等三角形的判定与性质,等腰直角三角形,解直角三角形
专题:
分析:(1)作∠DAH=∠EAB交DE于点H,得到∠DAB=∠HAE,再根据三角形的内角的和定理求出∠ABD=∠AEH,然后利用“角边角”证明△ABD和△AEH全等,根据全等三角形对应边相等可得BD=EH,AD=AH,再利用∠EAB=60°判断出△ADH是等边三角形,根据等边三角形的性质可得AD=HD,然后根据ED=HD+EH等量代换即可得证;
(2)方法同(1),利用α和AD表示出DH,然后写出答案即可;
(3)作∠DAH=∠EAB交DE于点H,得到∠DAB=∠HAE,再根据三角形的内角和定理求出∠ABD=∠AEH,然后利用“角边角”证明△ABD和△AEH全等,根据全等三角形对应边相等可得BD=EH,AD=AH,然后求出△ADH是等腰直角三角形,根据等腰直角三角形的性质可得
AD=HD,再根据ED=EH-HD等量代换即可得证.
(2)方法同(1),利用α和AD表示出DH,然后写出答案即可;
(3)作∠DAH=∠EAB交DE于点H,得到∠DAB=∠HAE,再根据三角形的内角和定理求出∠ABD=∠AEH,然后利用“角边角”证明△ABD和△AEH全等,根据全等三角形对应边相等可得BD=EH,AD=AH,然后求出△ADH是等腰直角三角形,根据等腰直角三角形的性质可得
| 2 |
解答: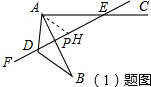 (1)证明:作∠DAH=∠EAB交DE于点H,
(1)证明:作∠DAH=∠EAB交DE于点H,
∴∠DAB=∠HAE,
∵∠EAB=∠EDB,∠APE=∠BPD,
∴∠ABD=∠AEH,
在△ABD和△AEH中,
,
∴△ABD≌△AEH(ASA),
∴BD=EH,AD=AH.,
∵∠DAH=∠EAB=60°,
∴△ADH是等边三角形,
∴AD=HD,
∵ED=HD+EH,
∴ED=AD+BD;
(2)方法同(1),
∵∠DAH=∠EAB=α,
∴HD=2ADsin
,
∴ED=2ADsin
+BD;
(3)ED=BD-
AD.
如图,作∠DAH=∠EAB交DE于点H,
∴∠DAB=∠HAE,
∵∠EDB=∠EAB=90°,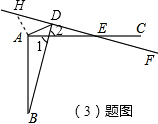
∴∠ABD+∠1=∠AEH+∠2=90°,
∵∠1=∠2,
∴∠ABD=∠AEH,
在△ABD和△AEH中,
,
∴△ABD≌△AEH(ASA),
∴BD=EH,AD=AH,
∵∠DAH=∠EAB=90°,
∴△ADH是等腰直角三角形,
∴HD=
AD,
∵ED=EH-HD,
∴ED=BD-
AD.
 (1)证明:作∠DAH=∠EAB交DE于点H,
(1)证明:作∠DAH=∠EAB交DE于点H,∴∠DAB=∠HAE,
∵∠EAB=∠EDB,∠APE=∠BPD,
∴∠ABD=∠AEH,
在△ABD和△AEH中,
|
∴△ABD≌△AEH(ASA),
∴BD=EH,AD=AH.,
∵∠DAH=∠EAB=60°,
∴△ADH是等边三角形,
∴AD=HD,
∵ED=HD+EH,
∴ED=AD+BD;
(2)方法同(1),
∵∠DAH=∠EAB=α,
∴HD=2ADsin
| α |
| 2 |
∴ED=2ADsin
| α |
| 2 |
(3)ED=BD-
| 2 |
如图,作∠DAH=∠EAB交DE于点H,
∴∠DAB=∠HAE,
∵∠EDB=∠EAB=90°,

∴∠ABD+∠1=∠AEH+∠2=90°,
∵∠1=∠2,
∴∠ABD=∠AEH,
在△ABD和△AEH中,
|
∴△ABD≌△AEH(ASA),
∴BD=EH,AD=AH,
∵∠DAH=∠EAB=90°,
∴△ADH是等腰直角三角形,
∴HD=
| 2 |
∵ED=EH-HD,
∴ED=BD-
| 2 |
点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,解直角三角形,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形和等边三角形是解题的关键,此类题目,往往都是求解思路相同,只是根据条件的变化结论稍作变更.

练习册系列答案
相关题目
 如果某物体的三视图如图,那么该物体的形状是( )
如果某物体的三视图如图,那么该物体的形状是( )| A、正方体 | B、长方体 |
| C、三棱柱 | D、圆锥 |
把不等式组
的解集在数轴上表示正确的是( )
|
A、 |
B、 |
C、 |
D、 |
 在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=
在?ABCD中,点E为AD的中点,连接BE,交AC于点F,AF=3,则AC=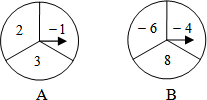 如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.
如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,且m=xy.
 初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题:
初三学生小英、小亮为了解本校820名初二学生每周体育锻炼的情况,各自在本校进行了抽样调查.小英调查了初二年级体育爱好者中40名学生每周体育锻炼的时间,算得这些学生平均每周锻炼时间为7.5小时;小亮从全体初二学生名单中随机抽取了40名学生,调查了他们每周锻炼的时间,算得这些学生平均每周锻炼时间为5.8小时.小英与小亮整理各自样本数据,如表所示.请根据上述信息,回答下列问题: