题目内容
10. 如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.
如图,AB为⊙O的直径,C为⊙O外一点,且∠CAB=90°,BD是⊙O的弦,BD∥CO.(1)求证:CD是⊙O的切线.
(2)若AB=4,AC=3,求BD的长.
分析 (1)连接OD,易证△CAO≌△CDO(SAS),由全等三角形的性质可得∠CDO=∠CAO=90°,即CD⊥OD,进而可证明CD是⊙O的切线.
(2)过点O作OE⊥BD,垂足为E,首先利用勾股定理可求出OC的长,再证明△OEB∽△CAO,由相似三角形的性质可求出BE的长,进而可求出BD的长.
解答 解:
(1)证明:如图,连接OD.
∵BD∥CO,
∴∠DBO=∠COA,∠ODB=∠COD.
在☉O中,OB=OD,
∴∠DBO=∠ODB.
∴∠COA=∠COD.
在△CAO和△CDO中,
$\left\{\begin{array}{l}{OA=OD}\\{∠COA=∠COD}\\{CO=CO}\end{array}\right.$
∴△CAO≌△CDO(SAS).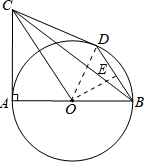
∴∠CDO=∠CAO=90°.
即 CD⊥OD.
又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)解:如图,过点O作OE⊥BD,垂足为E.
在⊙O中,OE⊥BD,
∴BE=DE.
在Rt△CAO中,OC=$\sqrt{32+22}$=$\sqrt{13}$.
∵∠COA=∠OBE,∠CAO=∠OEB,
∴△OEB∽△CAO.
∴$\frac{OA}{BE}$=$\frac{CO}{OB}$.
∴$\frac{2}{BE}$=$\frac{\sqrt{13}}{2}$.
∴BE=$\frac{4\sqrt{13}}{13}$.
∴BD=2BE=$\frac{8\sqrt{13}}{13}$.
点评 本题考查了切线的判断和性质、全等三角形的判断和性质、相似三角形的判断和性质以及勾股定理的运用,正确作出辅助线是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.下列轴对称图形中,对称轴的数量小于3的是( )
| A. |  | B. |  | C. |  | D. |  |
20.李老师对本班40名学生的A,B,O,AB四种血型作了统计,列出如下的统计表,则本班A型血的人数是( )个.
| 组别 | A型 | B型 | AB型 | O型 |
| 频数 | b | c | d | 6 |
| 频率 | a | 0.35 | 0.1 | e |
| A. | 16人 | B. | 14人 | C. | 4人 | D. | 6人 |
 已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.
已知:点D是等腰直角三角形ABC斜边BC上一点(不与点B重合),连接AD,将线段AD绕点A逆时针方向旋转90°得到线段AE,连接CE.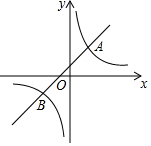 如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.
如图,在平面直角坐标系中,一次函数y=kx+b的图象与反比例函数y=mx-1的图象交于A(2,3),B(-3,n)两点.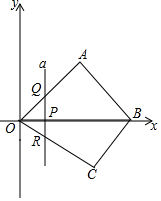 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.