题目内容
4.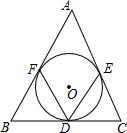 如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.
如图,⊙O是△ABC的内切圆,切点分别为D、E、F,∠B=60°,∠C=70°,求∠EDF的度数.
分析 连接OE,OF.由三角形内角和定理可求得∠A=50°,由切线的性质可知:∠OFA=90°,∠OEA=90°,从而得到∠A+∠EOF=180°,故可求得∠EOF=130°由圆周角定理可求得∠EDF=65°.
解答 解:如图所示;连接OE,OF.
∵∠B=60°,∠C=70°,
∴∠A=180°-60°-70°=50°.
∵AB是圆O的切线,
∴∠OFA=90°.
同理∠OEA=90°.
∴∠A+∠EOF=180°.
∴∠EOF=130°.
∴∠EDF=65°.
点评 本题主要考查的是切线的性质、三角形、四边形的内角和、圆周角定理,求得∠EOF的度数是解题的关键.

练习册系列答案
相关题目
14.一个容量为110的样本最大值是152,最小值是50,取组距为10,则可以分为( )
| A. | 9组 | B. | 10组 | C. | 11组 | D. | 12组 |
15.“十一”黄金周期间,某风景区在7天假期中每天旅游的人数变化如表(正数表示比前一天多的人数,负数表示比前一天少的人数)(单位:万人)
(1)请判断七天内游客人数最多的是哪天?最少的是哪天?它们相差多少万人?
(2)若9月30日该景区的游客人数为2万人,景区门票原价80元/人,这七天景区门票总收入是多少万元?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(2)若9月30日该景区的游客人数为2万人,景区门票原价80元/人,这七天景区门票总收入是多少万元?
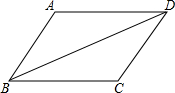 如图,△ABD≌△CDB,若AB=4,AD=5,则BC=5.
如图,△ABD≌△CDB,若AB=4,AD=5,则BC=5.