题目内容
1.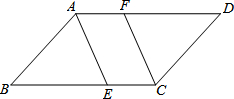 已知:如图,在?ABCD中,AE、CF分别平分∠BAD、∠BCD,AE、CF分别交BC、AD于点E、F.求证:AE∥CF.
已知:如图,在?ABCD中,AE、CF分别平分∠BAD、∠BCD,AE、CF分别交BC、AD于点E、F.求证:AE∥CF.
分析 先由角平分线的定义和平行四边形的性质得出∠DAE=∠BCF,再由平行线得出∠DAE=∠BEA,得出∠BEA=∠BCF,即可得出AE∥CF.
解答 证明:∵AE、CF分别平分∠BAD、∠BCD,
∴∠BAE=∠DAE=$\frac{1}{2}$∠BAD,∠BCF=∠DCF=$\frac{1}{2}$∠BCD,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AD∥BC,
∴∠DAE=∠BCF,
∵AD∥BC,∴∠DAE=∠BEA,
∴∠BEA=∠BCF,
∴AE∥CF.
点评 本题考查了平行四边形的性质、角平分线的定义以及平行线的性质与判定;弄清各个角之间的关系是解决问题的关键.

练习册系列答案
相关题目
6.若m与-3互为倒数,则m等于( )
| A. | -3 | B. | -$\frac{1}{3}$ | C. | $\frac{1}{3}$ | D. | 3 |
13.已知点A(n2+1,n)在正比例函数y=-2x的图象上,则( )
| A. | n>0 | B. | n<0 | C. | n≥-2 | D. | n≤-2 |
10.设a,b,c△ABC的三边长,则$\sqrt{(a+b-c)^{2}}$+|a-b-c|=( )
| A. | 2a-2c | B. | 2b | C. | 2c-2a | D. | 2a+2b |
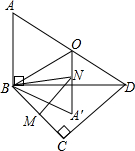 如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.
如图,一副三角板△BCD拼在一起,O为AD的中点,AB=4,将△ABO沿BO对折到△A′BO处,M为边BC上一动点,N为直线A′O一动点,则NB+NM的最小值为2$\sqrt{6}$.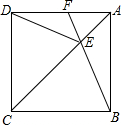 如图,正方形ABCD中,点E在对角线AC上,连接EB、ED.
如图,正方形ABCD中,点E在对角线AC上,连接EB、ED. 如图,菱形ABCD的对角线AC、BD交于点O,E为边BC的中点,若OE=6cm,则菱形ABCD的周长为48cm.
如图,菱形ABCD的对角线AC、BD交于点O,E为边BC的中点,若OE=6cm,则菱形ABCD的周长为48cm.