题目内容
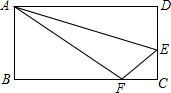 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.考点:翻折变换(折叠问题),勾股定理
专题:
分析:由四边形ABCD为矩形,AB=6cm,BC=10cm,又由折叠的性质,即可得AF=AD,然后在Rt△ABF中,利用勾股定理求得BF的长,即可得CF的长,然后设CE=xcm,在Rt△FCE中,由勾股定理即可得方程:(6-x)2=22+x2,解此方程即可求得CE的长
解答:解:∵△AFE是由△ADE折叠得到,
∴AF=AD=10cm,FE=DE,
在Rt△ABF中,BF=
=
=8cm,
∴CF=2cm,
设CE=xcm,则FE=DE=(6-x)cm,
在Rt△FCE中,FE2=EC2+FC2,即(6-x)2=22+x2,
解得x=
,
即CE=
cm.
∴AF=AD=10cm,FE=DE,
在Rt△ABF中,BF=
| AF2-AB2 |
| 102-62 |
∴CF=2cm,
设CE=xcm,则FE=DE=(6-x)cm,
在Rt△FCE中,FE2=EC2+FC2,即(6-x)2=22+x2,
解得x=
| 8 |
| 3 |
即CE=
| 8 |
| 3 |
点评:本题考查了折叠的性质,矩形的性质以及勾股定理.此题难度适中,解题的关键是注意数形结合思想与方程思想的应用,注意折叠中的对应关系.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
 如图,已知圆O与圆O′相交于点A、B,AB是⊙O的内接正三角形的一边,又是圆O′的内接正四边形的一边,且AB=2cm,求OO′的长.
如图,已知圆O与圆O′相交于点A、B,AB是⊙O的内接正三角形的一边,又是圆O′的内接正四边形的一边,且AB=2cm,求OO′的长. 如图,线段BD=
如图,线段BD= 如图,在△ABC中,BC=4,AC=2
如图,在△ABC中,BC=4,AC=2 如图,A、B是双曲线y=
如图,A、B是双曲线y=