题目内容
9．在Rt△ABC，若CD是Rt△ABC斜边AB上的高，AD=3，CD=4，则BC=$\frac{20}{3}$．分析 根据射影定理求出BD的长，再根据射影定理计算即可．
解答 
解：如图所示：∵CD是Rt△ABC斜边CD上的高，
∴CD2=AD•DB，
则16=3BD
故BD=$\frac{16}{3}$，
可得AB=AD+BD=$\frac{25}{3}$，
∵BC2=BD•BA=$\frac{16}{3}$×$\frac{25}{3}$，
∴BC=$\frac{20}{3}$，
故答案为：$\frac{20}{3}$．
点评 本题考查的是射影定理的应用，射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
2．式子（11+6$\sqrt{2}$）的算术平方根是（ ）
| A． | 3-$\sqrt{2}$ | B． | 3+$\sqrt{2}$ | C． | 3$\sqrt{2}$ | D． | -3-$\sqrt{2}$ |
3．
将一些相同的图形“●”按如图所示的规律依次摆放，观察每个图形中“●”的个数，若第n个图形中有3008个“●”，则n的值是（ ）
将一些相同的图形“●”按如图所示的规律依次摆放，观察每个图形中“●”的个数，若第n个图形中有3008个“●”，则n的值是（ ）| A． | 996 | B． | 999 | C． | 1001 | D． | 1002 |
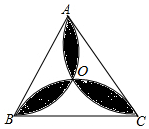如图，在边长为a的等边三角形ABC中有一个由三个全等的叶形所组成的“三叶草”图形，点O是△ABC的外心，则该“三叶草”图形的面积是$\frac{π}{3}$a2-$\frac{\sqrt{3}}{2}$a2．
1．下列与：-9+31+28-45相等的是（ ）
| A． | -9+45+28-31 | B． | 31-45-9+28 | C． | 28-9-31-45 | D． | 45-9-28+31 |
