题目内容
4.已知函数y1=a1x2和函数y2=a2x2满足a1a2>0,且当y1=y2=y0时,y1,y2对应的一个自变量的值分别是x1,x2,且|x1|>|x2|,试比较|a1|,|a2|的大小.分析 根据题意判断函数y1=a1x2和函数y2=a2x2开口方向相同,函数y1=a1x2的开口较大,从而根据二次函数的性质判定|a1|<|a2|.
解答 解:∵函数y1=a1x2和函数y2=a2x2满足a1a2>0,
∴a1,a2的符号相同,
∴函数y1=a1x2和函数y2=a2x2开口方向相同,
∵|x1|>|x2|,
∴函数y1=a1x2的开口较大,
∴|a1|较小,
∴|a1|<|a2|.
点评 本题考查了二次函数图象上点的坐标特征以及二次函数的性质,二次函数图象开口的大小取决于二次项系数的绝对值的大小,绝对值越大开口越小.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.某商场第一季度的利润为82.75万元.其中一月份的利润是25万元,则平均每月利润的增长率为( )
| A. | 10% | B. | 15% | C. | 12% | D. | 8% |
 如图,AB=CD,BD=AC,AB∥CD,求证:AB⊥BC.
如图,AB=CD,BD=AC,AB∥CD,求证:AB⊥BC. 如图(1)(2)的截面形状是三角形,四边形.
如图(1)(2)的截面形状是三角形,四边形.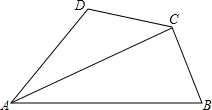 已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论.
已知,四边形ABCD中,∠D与∠B互补,且对角线AC平分∠BAD,请比较BC与DC的大小,并证明你的结论. 如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)
如图,如果$\frac{AC}{AB}$=$\frac{CB}{AC}$,那么点C叫做线段AB的黄金分割点,$\frac{AC}{AB}$也就成为黄金分割比,你能算出这个比值吗?($\sqrt{5}$≈2.236)