题目内容
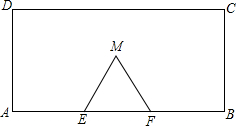 如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm;
如图:在矩形ABCD中,AD=60cm,CD=120cm,E、F为AB边的三等分点,以EF为边在矩形内作等边三角形MEF,N为AB边上一点,EN=10cm;请在矩形内找一点P,使△PMN为等边三角形(画出图形,并直接写出△PMF的面积).
考点:矩形的性质,等边三角形的判定与性质,作图—应用与设计作图
专题:
分析:如图,以MN为边容易作出等边三角形,结合等边三角形的性质,连接PE,可证明△MPE≌△MNF,可证明PE∥MF,容易求得S△PMF=S△MEF,可求得答案.
解答: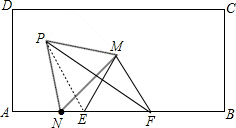 解:如图,以MN为边,可作等边三角形PMN;
解:如图,以MN为边,可作等边三角形PMN;
△PMF的面积为400
.(求解过程如下).
连接PE,
∵△MEF和△PMN为等边三角形,
∴∠PMN=∠NMF=∠MFE=60°,MN=MP,NE=NF,
∴∠PME=∠NMF,
在△MPE和△MNF中,
,
∴△MPE≌△MNF(SAS),
∴∠MEP=∠MFE=60°,
∴∠PEN=60°,
∴PE∥MF,
∴S△PMF=S△MEF=
EF2=400
.
 解:如图,以MN为边,可作等边三角形PMN;
解:如图,以MN为边,可作等边三角形PMN;△PMF的面积为400
| 3 |
连接PE,
∵△MEF和△PMN为等边三角形,
∴∠PMN=∠NMF=∠MFE=60°,MN=MP,NE=NF,
∴∠PME=∠NMF,
在△MPE和△MNF中,
|
∴△MPE≌△MNF(SAS),
∴∠MEP=∠MFE=60°,
∴∠PEN=60°,
∴PE∥MF,
∴S△PMF=S△MEF=
| ||
| 4 |
| 3 |
点评:本题主要考查等边三角形的性质及全等三角形的性质和判定,利用全等证得PE∥MF,得到S△PMF=S△MEF是解题的关键.

练习册系列答案
相关题目
 下列说法正确的是( )
下列说法正确的是( )| A、射线AB和射线BA表示的是同一条射线 |
| B、直线AB和直线BA表示的是两条直线 |
| C、线段AB和线段BA表示的是同一条线段 |
| D、如图,点M在直线AB上,则点M在射线AB上 |
用尺规作图,下列条件能作出唯一三角形的有( )
①已知两锐角;②已知两边及夹角;③已知三边;④已知两角及一边.
①已知两锐角;②已知两边及夹角;③已知三边;④已知两角及一边.
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上是该图形能折面一个密封的正方体的盒子,共有
如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上是该图形能折面一个密封的正方体的盒子,共有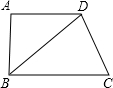 如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=BD.
如图,在梯形ABCD中,AD∥BC,∠ABC=90°,BC=BD. 在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论:
在梯形ABCD中,AB∥DC,AB<DC,点P为BD中点,记S△APB=S1,S△PDC=S2,梯形ABCD的面积为S,下面四个结论: