题目内容
如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.
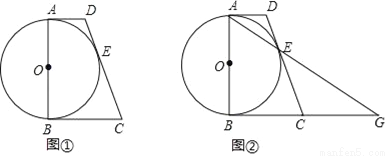
(1)求证:BC为⊙O的切线;
(2)连接AE并延长与BC的延长线交于点G(如图②所示).若AB=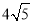 ,CD=9,求线段BC和EG的长.
,CD=9,求线段BC和EG的长.
练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
题目内容
如图①,AB为⊙O的直径,AD与⊙O相切于点A,DE与⊙O相切于点E,点C为DE延长线上一点,且CE=CB.

(1)求证:BC为⊙O的切线;
(2)连接AE并延长与BC的延长线交于点G(如图②所示).若AB=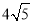 ,CD=9,求线段BC和EG的长.
,CD=9,求线段BC和EG的长.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案