题目内容
3.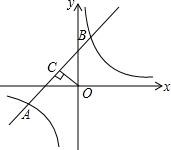 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{k}{x}$的图象与一次函数y=x+2的图象的一个交点为A(m,-1).(1)求反比例函数的解析式;
(2)设一次函数y=x+2的图象与y轴交于点B,OC⊥AB,垂足为C,求OC的长.
分析 (1)把A点坐标代入直线可求得m,可求得A点坐标,再把A点坐标代入反比例函数解析式,根据待定系数法求得反比例函数解析式;
(2)设直线y=x+2与x轴的交点为D,可求得OB=OD,可判断△BOD为等腰直角三角形,再根据直角三角形的性质可求得OC.
解答 解:(1)∵A在y=x+2上,
∴-1=m+2,解得m=-3,
∴A(-3,-1),
∵A在y=$\frac{k}{x}$上,
∴-1=$\frac{k}{-3}$,解得k=3,
∴反比例函数解析式为y=$\frac{3}{x}$;
(2)在y=x+2中,令x=0,可得y=2,
∴B(0,2),
如图,设直线y=x+2与x轴交于点D,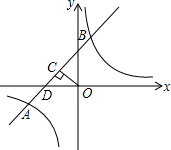
则D(-2,0),
∴OB=OD=2,
∵OC⊥AB,
∴∠DOC=∠BOC=∠OBC=45°,
∴OC=BC,
在Rt△BOC中,OB2=OC2+BC2,
∴22=2OC2,
∴OC=$\sqrt{2}$.
点评 本题主要考查一次函数和反比例函数的交点问题,在(1)中注意待定系数法的应用,在(2)中求得△BOD为等腰直角三角形是解题的关键.

练习册系列答案
相关题目
18.下列事件:①在足球赛中,弱队战胜强队;②抛掷一枚硬币,落地正面朝上;③任取两个负数,其积大于0;④长分别为3、5、9厘米的三条线段不能围成一个三角形.其中确定事件的个数是( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
8.我国南海海域面积为3800000km2,用科学记数法表示正确的是( )
| A. | 3.8×105km2 | B. | 3.8×106km2 | C. | 3.8×107km2 | D. | 3.8×108km2 |
15.在学校组织的游艺晚会上,掷飞标游艺区游戏区规则如下,如图掷到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点)现统计小华、小明和小芳掷中与得分情况,如图所示,依此方法计算小芳的得分为( )
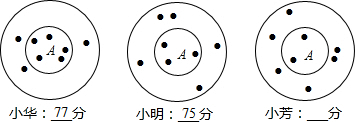

| A. | 76 | B. | 74 | C. | 72 | D. | 70 |
12.不等式-3x<6的解集为( )
| A. | x<-2 | B. | x>-2 | C. | x<2 | D. | x>2 |
8.实数4的倒数是( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | -$\frac{1}{4}$ |
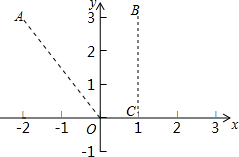 对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.
对于两个已知图形G1、G2,在G1上任取一点P,在G2上任取一点Q,当线段PQ的长度最小时,我们称这个最小的长度为G1、G2的“密距”.如图,A(-2,3),B(1,3),C(1,0),则点A与射线OC之间的“密距”为$\sqrt{13}$,点B与射线OC之间的“密距”为3,如果直线y=x-1和双曲线y=$\frac{k}{x}$之间的“密距”为$\frac{3\sqrt{2}}{2}$,则k的值为-4.