Question

5．已知半径为10的⊙O中的弦AB与弦CD平行，AB=12，CD=16，M，N分别为AB，CD的中点，则MN=2或14．

Answer 1

分析 根据垂径定理证明M、O、N在同一条直线上，分两种情况进行讨论：①弦AB和CD在圆心同侧；②弦AB和CD在圆心异侧；作出半径和弦心距，利用勾股定理和垂径定理求解即可．

解答 解：∵连接OM、ON，
∵M，N分别为AB，CD的中点，
∴OM⊥AB，ON⊥CD，
∵AB∥CD，
∴M、O、N在同一条直线上，
当弦AB和CD在圆心同侧时，如图1，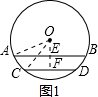
∵AB=16，CD=12，
∴AM=8，CN=6，
∵OA=OC=10，
∴MO=6，ON=8，
∴MN=ON-OM=2；
当弦AB和CD在圆心异侧时，如图2，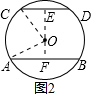
∵AB=16，CD=12，
∴AM=8，CN=6，
∵OA=OC=10，
∴MO=6，ON=8，
∴MN=ON+OM=14，
故答案为：2或14．

点评 本题考查了勾股定理和垂径定理，解此类题目要注意将圆的问题转化成三角形的问题再进行计算．