Question

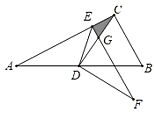
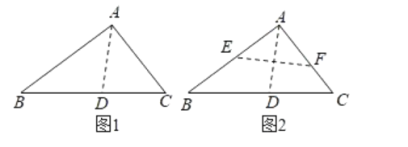
【题目】如图，将直角三角形纸片（，）沿过点A的直线折叠，使得AC落在AB边上折痕为AD，展开纸片（如图1）；再次折叠该三角形纸片，使点A和点D重合，折痕为EF，展平纸片后得到（如图2），若，，则折痕EF的长为（ ）

A.B.C.D.5

Answer 1

【答案】A

【解析】

如图，连接DE，DF，先证四边形AEDF是正方形，可得AE=AF=DE=DF，EF=DE，由面积法可求DE的长，即可求解．

解：如图，连接DE，DF，

由折叠的性质可得：∠BAD=∠CAD=∠BAC=45°，

AE=DE，AF=DF，AD⊥EF，

∴∠EAD=∠EDA=45°，∠FAD=∠FDA=45°，

∴∠AED=∠AFD=90°=∠BAC，

∴四边形AEDF是矩形，

又∵AD⊥EF，

∴四边形AEDF是正方形，

∴AE=AF=DE=DF，EF=DE，

∵，

∴6×8=14DE，

∴DE=， ∴EF=，

故选：A．