题目内容
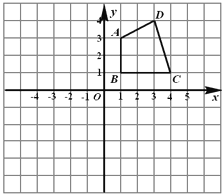
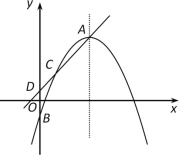
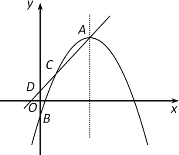
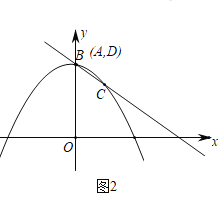
【题目】如图,在平面直角坐标系中,已知二次函数![]() 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
(1)当m=5时,求n的值.
(2)当n=2时,若点A在第一象限内,结合图象,求当y![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
(3)作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
【答案】(1)-4(2)1≤x≤5(3)0≤m<1或1<m<2![]()
【解析】
1)利用待定系数法求解即可.
(2)求出![]() 时,
时,![]() 的值即可判断.
的值即可判断.
(3)由题意点![]() 的坐标为
的坐标为![]() ,求出几个特殊位置
,求出几个特殊位置![]() 的值即可判断.
的值即可判断.
解:(1)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
(2)当![]() 时,将
时,将![]() 代入函数表达式
代入函数表达式![]() ,得
,得![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 此时抛物线的对称轴
此时抛物线的对称轴![]() ,
,
根据抛物线的对称性可知,当![]() 时,
时,![]() 或5,
或5,
![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() 点
点![]() 与点
与点![]() 不重合,
不重合,
![]() ,
,
![]() 抛物线的顶点
抛物线的顶点![]() 的坐标是
的坐标是![]() ,
,
![]() 抛物线的顶点在直线
抛物线的顶点在直线![]() 上,
上,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
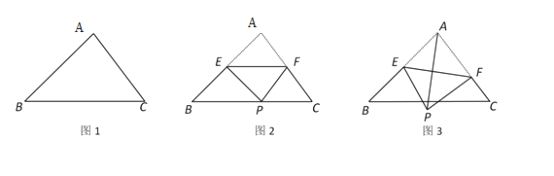
抛物线从图1的位置向左平移到图2的位置,![]() 逐渐减小,点
逐渐减小,点![]() 沿
沿![]() 轴向上移动,
轴向上移动,
当点![]() 与
与![]() 重合时,
重合时,![]() ,
,
解得![]() 或
或![]() ,
,
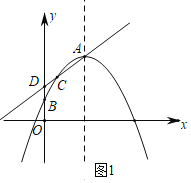
当点![]() 与点
与点![]() 重合时,如图2,顶点
重合时,如图2,顶点![]() 也与
也与![]() ,
,![]() 重合,点
重合,点![]() 到达最高点,
到达最高点,
![]() 点
点![]() ,
,
![]() ,解得
,解得![]() ,
,
当抛物线从图2的位置继续向左平移时,如图3点![]() 不在线段
不在线段![]() 上,
上,
![]() 点在线段
点在线段![]() 上时,
上时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目