题目内容
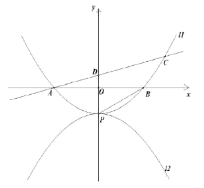
【题目】如图,直线y=![]() x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=
x+c与x轴交于点B(4,0),与y轴交于点C,抛物线y=![]() x2+bx+c经过点B,C,与x轴的另一个交点为点A.
x2+bx+c经过点B,C,与x轴的另一个交点为点A.
(1)求抛物线的解析式;
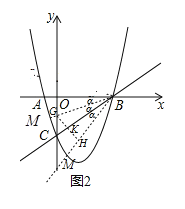
(2)点P是直线BC下方的抛物线上一动点,求四边形ACPB的面积最大时点P的坐标;
(3)若点M是抛物线上一点,请直接写出使∠MBC=![]() ∠ABC的点M的坐标.
∠ABC的点M的坐标.

【答案】(1)y=![]() x2﹣
x2﹣![]() x﹣3;(2)点P(2,﹣
x﹣3;(2)点P(2,﹣![]() );(3)
);(3)![]() 或
或![]() .
.
【解析】
(1)将点B坐标代入![]() 并解得:
并解得:![]() ,故抛物线的表达式为:
,故抛物线的表达式为:![]() ,将点B坐标代入上式,即可求解;
,将点B坐标代入上式,即可求解;
(2)因为S四边形ACPB=S△AOC+S△PCB,∵S△AOC是常数,故四边形面积最大,只需要S△PCB最大即可,S△PCB= ![]() ,即可求解;
,即可求解;
(3)过点B作∠ABC的角平分线交y轴于点G,交抛物线于M,利用角平分线的性质求出![]() 的坐标,进而求直线
的坐标,进而求直线![]() 的解析式,联立解析式解方程组即可得到一个答案,利用角的对称性求出
的解析式,联立解析式解方程组即可得到一个答案,利用角的对称性求出![]() 在
在![]() 下方时
下方时![]() 关于
关于![]() 的对称点
的对称点![]() ,求出直线
,求出直线![]() 的解析式,即可联立解析式求解.
的解析式,即可联立解析式求解.
解:(1)将点B坐标代入![]() 并解得:c=﹣3,
并解得:c=﹣3,
故抛物线的表达式为:![]() ,
,
将点B坐标代入上式并解得:![]() ,
,
故抛物线的表达式为:y=![]() x2﹣
x2﹣![]() x﹣3;
x﹣3;
(2)过点P作PH∥y轴交BC于点H,
设点![]() ,则点
,则点![]() ,
,
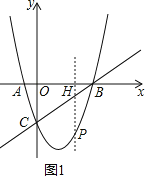
S四边形ACPB=S△ABC+S△PCB,
∵S△ABC是常数,故四边形面积最大,只需要S△PCB最大即可,
S△PCB=![]() ×OB×PH=
×OB×PH=![]() ,
,
∵![]() <0,∴S△PCB有最大值,此时,点P(2,﹣
<0,∴S△PCB有最大值,此时,点P(2,﹣![]() );
);
(3) 过点B作∠ABC的角平分线交y轴于点G,交抛物线于M,
因为:![]() ,所以:
,所以:![]() ,
,
由角平分线的性质得:![]() 所以:
所以:![]() ,
,
解得:![]() ,所以:
,所以:![]() ,
,
设![]() 为:
为:![]() ,所以:
,所以:
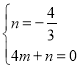 ,解得:
,解得: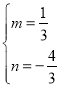 ,
,
所以![]() 为:
为:![]() ,
,
所以: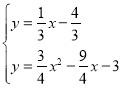 ,
,
解得: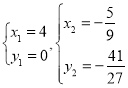 ,
,
所以:此时M![]()
过点G作GK⊥BC交BC于点K,延长GK交BM于点H,使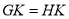 ,
,
则![]() ,BC是GH的中垂线, OB=4,OC=3,则BC=5,
,BC是GH的中垂线, OB=4,OC=3,则BC=5,
在Rt△GCK中,![]() ,
,![]() ,
,
则cos∠CGK=![]() ,sin∠CGK=
,sin∠CGK=![]() ,
,
则点![]() ,
,
因为点K是点GH的中点,
则点![]() ,
,
则直线BH的表达式为:![]() ,
,
所以: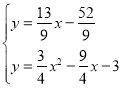 ,
,
解得: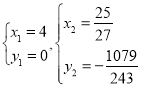 ,
,
所以:![]() .
.
综上:![]() 或
或![]() .
.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案