题目内容
如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，交AC于D，沿DE所在直线折叠，使点B恰好与点A重合，若CD=2，则DE的值为考点：翻折变换（折叠问题）
专题：
分析：根据折叠的性质可知DE⊥AB，根据角平分线的性质即可得到DE的值．
解答：解：∵沿DE所在直线折叠，使点B恰好与点A重合，
∴DE⊥AB，
∵BD平分∠ABC，∠C=90°，
∴DE=CD=2．
故答案为：2．
∴DE⊥AB，
∵BD平分∠ABC，∠C=90°，
∴DE=CD=2．
故答案为：2．
点评：此题考查了折叠的性质以及角平分线的性质．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想的应用．
练习册系列答案
相关题目
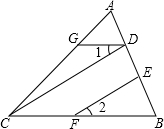已知：如图，∠AGD=∠ACB，∠1=∠2，CD与EF平行吗？为什么？
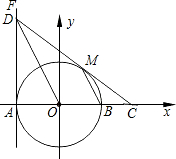如图，在平面直角坐标系xOy中，⊙O交x轴于A、B两点，直线FA⊥x轴于点A，点D在FA上，且点D的坐标为（-2，4），DO平行⊙O的弦MB，连DM并延长交x轴于点C．
如图，△ABC为等腰直角三角形，∠C=90°，AC=6．动点O在△ABC的边上，从点A出发沿着A→C→B→A的路线匀速运动一周，速度为1个长度单位每秒，以O为圆心、半径为1的圆在运动过程中与△ABC的边BC相切时是出发后第