题目内容
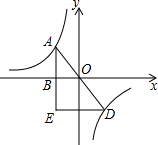 如图,反比例函数y1=
如图,反比例函数y1=| k |
| x |
| 3 |
| 3 |
(1)求m与k的值;
(2)若过A点的直线y2=ax+b与x轴正半轴交于C点,且∠ACO=30°,求直线解析式;
(3)当y1>y2时,请直接写出自变量x的取值范围.
考点:反比例函数综合题,待定系数法求一次函数解析式,反比例函数与一次函数的交点问题,相似三角形的判定与性质
专题:综合题,数形结合
分析:(1)由对称性易得OA=OD=
AD,然后利用相似三角形的性质可求出△ABO的面积,从而得到k的值及m的值.
(2)由条件利用特殊角的三角函数值可求出点C的坐标,利用待定系数法就可求出直线的解析式.
(3)先求出直线与反比例函数的图象的交点坐标,然后利用图象就可解决问题.
| 1 |
| 2 |
(2)由条件利用特殊角的三角函数值可求出点C的坐标,利用待定系数法就可求出直线的解析式.
(3)先求出直线与反比例函数的图象的交点坐标,然后利用图象就可解决问题.
解答:解:(1)如图1,
∵直线AD与反比例函数y1=
的图象都关于原点对称,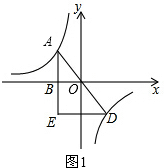
∴OA=OD=
AD.
∵DE⊥y轴,OB⊥y轴,
∴OB∥DE.
∴△ABO∽△AED.
∴
=(
)2=
.
∵S△AED=4
,
∴S△ABO=
.
∵AB⊥OB,
∴-
=
.
∴k=-2
.
∵反比例函数y1=
的图象经过点A(-
,m),
∴-
m=-2
.
∴m=2.
∴k的值为-2
,m的值为2.
(2)如图2,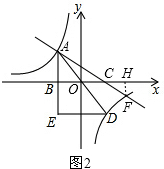
∵点A的坐标为(-
,2),
∴OB=
,AB=2.
∵AB⊥BC,∠ACB=30°,
∴tan30°=
=
=
.
∴BC=2
.
∴OC=
.
∴点C的坐标为(
,0).
设直线AC的解析式为y2=kx+b,
∴
.
解得:
.
∴直线AC的解析式为y2=-
x+1.
(3)设直线AC与反比例函数的图象的另一个交点为F,过点F作FH⊥x轴,垂足为H,如图2,
联立
,
解得:
或
.
∴点F的坐标为(2
,-1).
结合图象可得:当y1>y2时,x的取值范围是-
<x<0或x>2
.
∵直线AD与反比例函数y1=
| k |
| x |

∴OA=OD=
| 1 |
| 2 |
∵DE⊥y轴,OB⊥y轴,
∴OB∥DE.
∴△ABO∽△AED.
∴
| S△ABO |
| S△AED |
| AO |
| AD |
| 1 |
| 4 |
∵S△AED=4
| 3 |
∴S△ABO=
| 3 |
∵AB⊥OB,
∴-
| k |
| 2 |
| 3 |
∴k=-2
| 3 |
∵反比例函数y1=
| k |
| x |
| 3 |
∴-
| 3 |
| 3 |
∴m=2.
∴k的值为-2
| 3 |
(2)如图2,

∵点A的坐标为(-
| 3 |
∴OB=
| 3 |
∵AB⊥BC,∠ACB=30°,
∴tan30°=
| AB |
| BC |
| 2 |
| BC |
| ||
| 3 |
∴BC=2
| 3 |
∴OC=
| 3 |
∴点C的坐标为(
| 3 |
设直线AC的解析式为y2=kx+b,
∴
|
解得:
|
∴直线AC的解析式为y2=-
| ||
| 3 |
(3)设直线AC与反比例函数的图象的另一个交点为F,过点F作FH⊥x轴,垂足为H,如图2,
联立
|
解得:
|
|
∴点F的坐标为(2
| 3 |
结合图象可得:当y1>y2时,x的取值范围是-
| 3 |
| 3 |
点评:本题考查了直线与反比例函数的交点问题、用待定系数法求一次函数的解析式、相似三角形的判定与性质等知识,还考查了数形结合的思想,是一道好题.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
 如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数.
如图,已知∠1+∠2=180°,∠DEF=∠A,∠BED=60°,求∠ACB的度数. 如图,过点A画EF∥BC.
如图,过点A画EF∥BC. 如图,小岛A在港口P的南偏西37°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东50°方向,以18海里/时的速度驶离港口.现两船同时出发,
如图,小岛A在港口P的南偏西37°方向,距离港口81海里处.甲船从A出发,沿AP方向以9海里/时的速度驶向港口,乙船从港口P出发,沿南偏东50°方向,以18海里/时的速度驶离港口.现两船同时出发,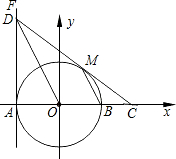 如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C.
如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且点D的坐标为(-2,4),DO平行⊙O的弦MB,连DM并延长交x轴于点C. 如图,?ABCD中,对角线AC平分∠DAB,判断?ABCD是菱形吗?并说明理由.
如图,?ABCD中,对角线AC平分∠DAB,判断?ABCD是菱形吗?并说明理由. 如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题:
如图,在甲、乙两同学进行的400米跑步比赛中,路程s(米)与时间t(秒)之间函数关系的图象分别为折线OAB和线段OC,根据图象提供的信息回答以下问题: