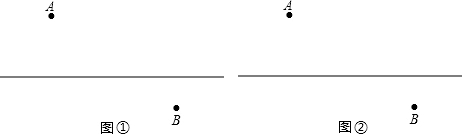题目内容
12. 如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.在直线AD上是否存在点P使得△AFP为等腰三角形?若存在,直接写出P点坐标;若不存在,请说明理由.
如图,在平面直角坐标系xOy中,正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,直线y=2x+2与y轴交于点E,与x轴交于点F.在直线AD上是否存在点P使得△AFP为等腰三角形?若存在,直接写出P点坐标;若不存在,请说明理由.
分析 由直线的解析式求得F的坐标,即可求得DF,根据勾股定理求得AF=5,然后分三种情况讨论求得即可.
解答 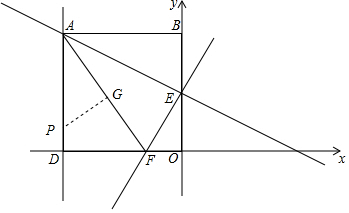 解:在直线AD上存在点P使得△AFP为等腰三角形;
解:在直线AD上存在点P使得△AFP为等腰三角形;
∵正方形ABOD的边OD,BO在坐标轴上,正方形边长为4,
∴OD=AD=4,
∵直线y=2x+2与y轴交于点E,与x轴交于点F.
∴F(-1,0),
∴OF=1,
∴DF=4-1=3,
∴在Rt△ADF中,AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=5,
①当AP=AF时,则P(-4,-1)或(-4,9)
②当AF=PF时,则P(-4,-4),
③当PA=PF时,取AF的中点G,作PG⊥AF,交AD于P,
∵∠AGP=∠ADF=90°,∠PAG=∠FAD,
∴△PAG∽△FAD,
∴$\frac{PA}{AF}$=$\frac{AG}{AD}$,即$\frac{PA}{5}$=$\frac{\frac{5}{2}}{4}$,
∴PA=$\frac{25}{8}$,
∴P(-4,$\frac{7}{8}$),
综上,P点坐标为(-4,-1)或(-4,9)或(-4,-4)或(-4,$\frac{7}{8}$).
点评 本题考查了一次函数图象上点的坐标特征,正方形的性质,等腰三角形的判定等,分类讨论思想的运用是解题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1.某自行车厂计划一周生产自行车1400辆,平均每天生产200辆,但由于种种原因,实际每天生产量与计划量相比有出入.如表是某周的生产情况(超产记为正、减产记为负):
(1)根据记录的数据可知该厂星期六生产自行车多少辆?
(2)产量最多的一天比产量最少的一天多生产多少辆自行车?
(3)求该厂本周实际生产自行车多少辆?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
(2)产量最多的一天比产量最少的一天多生产多少辆自行车?
(3)求该厂本周实际生产自行车多少辆?
 如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:
如图,C为射线AB上一点,AB=30,AC比BC的$\frac{1}{4}$多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: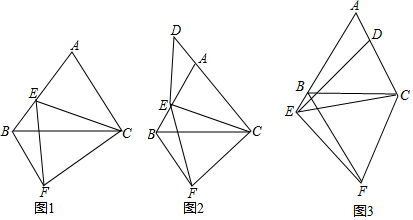
 如图所示,作出△ABC关于直线l的对称三角形A'B'C'.
如图所示,作出△ABC关于直线l的对称三角形A'B'C'.