Question

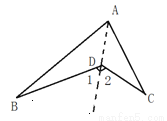
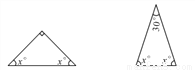
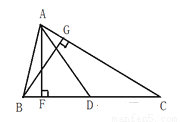
（本题共10分）AB和AC 相交于点A， BD和CD相交于点D，探究∠BDC与∠B 、 ∠C、∠BAC的关系．

小明是这样做的：

解：以点A为端点作射线AD．

∵∠1是△ABD的外角，∴∠1= ∠B+∠BAD．

同理∠2=∠C+∠CAD．

∴∠1+∠2=∠B+∠BAD+∠C+∠CAD．即∠BDC=∠B+∠C+∠BAC．

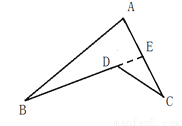
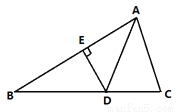
小英的思路是：延长BD交AC于点E．

（1）按小英的思路完成∠BDC=∠B+∠C+∠BAC这一结论．

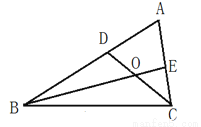
（2）按照上面的思路解决如下问题：如图：在△ABC中，BE、CD分别是∠ABC∠ACB的角平分线，交AC于E，交AB于D．BE、CD相交于点O，∠A=60°．求∠BOC的度数．

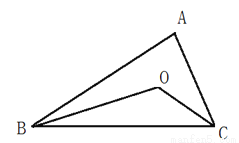
（3）如图：△ABC中，BO、CO分别是∠ABC与∠ACB的角平分线，且BO、CO相交于点O．猜想∠BOC与∠A有怎样的关系，并加以证明．

（1）证明见解析；（2）120°；（3）∠BOC=90°+ ∠A． 【解析】试题分析： （1）按小英的思路：∠BDC是△DCE的外角，∠DEC是△ABE的外角，则由三角形外角的性质可得；∠BDC=∠C+∠DEC，∠DEC=∠B+∠BAC，由此可得：∠BDC=∠C+∠B+∠BAC； （2）由△ABC中，BE、CD分别是∠ABC∠ACB的角平分线，交AC于E，交AB于D．BE、CD相...

Answer 1