题目内容
15.勾股定理神秘而每秒,它的证法多样,其巧妙各有不同,其中的”面积法“给小聪明以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程: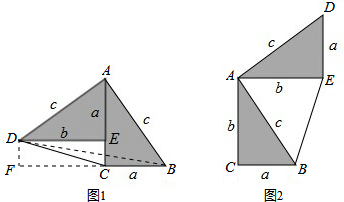
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2
证明:连接DB,过点D作BC边上的高DF,
则DF=EC=b-A.
∵S四边形ADCB=S△ACD+S△ABC=$\frac{1}{2}$b2+$\frac{1}{2}$ab.
又∵S四边形ADCB=S△ADB+S△DCB=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连结BD
∵S多边形ACBED=$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab
又∵S多边形ACBED=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a)
∴a2+b2=c2.
分析 连接BD,多边形ACBED的面积=△ABC的面积+△ABE的面积+△ADE的面积=$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,多边形ACBED的面积=△ABC的面积+△ABD的面积+△BDE的面积=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),得出$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),即可得出结论.
解答 解:连接BD,如图所示: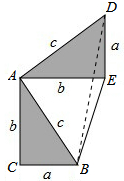
∵多边形ACBED的面积=△ABC的面积+△ABE的面积+△ADE的面积=$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,
又∵多边形ACBED的面积=△ABC的面积+△ABD的面积+△BDE的面积=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
∴$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),
整理得:a2+b2=c2.
故答案为:BD,$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab,$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a),$\frac{1}{2}ab$+$\frac{1}{2}$b2+$\frac{1}{2}$ab=$\frac{1}{2}$ab+$\frac{1}{2}$c2+$\frac{1}{2}$a(b-a).
点评 本题考查了勾股定理的证明、三角形面积的计算方法、多边形面积的计算方法;熟练掌握勾股定理的证明方法,运用面积法证明勾股定理是常用的方法.

 如图,分别求一个或一组平移,使得:
如图,分别求一个或一组平移,使得: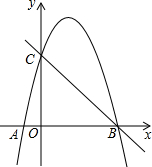 如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B.
如图,抛物线y=ax2+bx-4a经过A(-1,0)、C(0,4)两点,与x轴交于另一点B. 如图为抛物线y=ax2+bx+c,则4a-2b+c=0(值).
如图为抛物线y=ax2+bx+c,则4a-2b+c=0(值).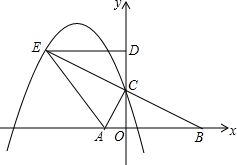 如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE.
如图,在平面直角坐标系中,已知点A(-1,0)和点B(4,0),点C在y轴正半轴上,且∠ACB=90°,将△COB绕点C旋转180°得到△CDE,连结AE. 如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.
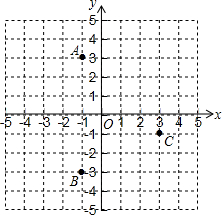
如图,长方形ABCD的长与宽分别是6,4,建立适当的直角坐标系,写出各顶点的坐标.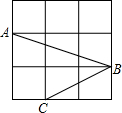 如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.
如图,网格中的每个小正方形的边长都是1,A,B,C三点是小正方形的顶点,则∠ABC的度数为45°.