题目内容
3.计算:(1)$\frac{{x}^{2}+x}{x}•\frac{2x}{x+1}$
(2)(1+$\frac{1}{x}$)$•\frac{x}{{x}^{2}-1}$
(3)$\frac{x}{x-y}•\frac{{y}^{2}}{x+y}-\frac{{x}^{4}y}{{x}^{4}-{y}^{4}}÷\frac{{x}^{2}}{{x}^{2}+{y}^{2}}$
(4)$\frac{a+3}{{a}^{2}-2a+1}$÷$(1+\frac{4}{a-1})$.
分析 (1)先因式分解,再约分即可;
(2)先计算括号里面的,再因式分解,再约分即可;
(3)先因式分解,再约分,最后算加减即可;
(4)先算括号里面的,再因式分解,约分即可;
解答 解:(1)原式=$\frac{x(x+1)}{x}$•$\frac{2x}{x+1}$
=2x;
(2)原式=$\frac{x+1}{x}$•$\frac{x}{(x+1)(x-1)}$
=$\frac{1}{x-1}$;
(3)原式=$\frac{{xy}^{2}}{(x-y)(x+y)}$-$\frac{{x}^{4}y}{{(x}^{2}+{y}^{2}{)(x}^{2}-{y}^{2})}$•$\frac{{x}^{2}+{y}^{2}}{{x}^{2}}$
=$\frac{{xy}^{2}}{(x-y)(x+y)}$-$\frac{{x}^{2}y}{{x}^{2}-{y}^{2}}$
=$\frac{{xy}^{2}-{x}^{2}y}{(x-y)(x+y)}$
=$\frac{-xy(x-y)}{(x-y)(x+y)}$
=-$\frac{xy}{x+y}$;
(4)原式=$\frac{a+3}{(a-1)^{2}}$÷$\frac{a+3}{a-1}$
=$\frac{a+3}{{(a-1)}^{2}}$•$\frac{a-1}{a+3}$
=$\frac{1}{a-1}$.
点评 本题考查的是分式的混合运算,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
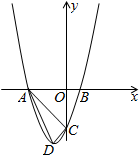 如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴相交于点C(0,-3)与x轴交于A、B两点(点A在点B的左边),连接AC、CD、AD.
如图,抛物线y=x2+bx+c的顶点为D(-1,-4),与y轴相交于点C(0,-3)与x轴交于A、B两点(点A在点B的左边),连接AC、CD、AD.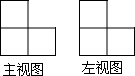 由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示.
由一些大小相同的小正方体组成的简单几何体的主视图和左视图如图所示. 如图,在?ABCD中,BE:EC=1:2,且S△BEF=2cm2,求S?ABCD.
如图,在?ABCD中,BE:EC=1:2,且S△BEF=2cm2,求S?ABCD.