题目内容
2．若二次函数y=（m2-4）x2+（m2-2m+24）x+6（m-6）的图象与x轴的正半轴相交于横坐标为整数的两个不同的点，试确定m的值．分析 根据二次函数y=（m2-4）x2+（m2-2m+24）x+6（m-6）的图象与x轴的正半轴相交于横坐标为整数的两个不同的点，可求得y=0时的x的值，且x的值为大于0的整数，从而可以解答本题．
解答 解：∵y=（m2-4）x2+（m2-2m+24）x+6（m-6），
∴y=[（m+2）x+（m-6）][（m-2）x+6]．
∴y=0时，[（m+2）x+（m-6）][（m-2）x+6]=0．
解得，${x}_{1}=-\frac{m-6}{m+2}，{x}_{2}=-\frac{6}{m-2}$．
∵二次函数y=（m2-4）x2+（m2-2m+24）x+6（m-6）的图象与x轴的正半轴相交于横坐标为整数的两个不同的点，
∴$-\frac{m-6}{m+2}$＞0且为整数，$-\frac{6}{m-2}＞0$且为整数．
解得m=0或m=-1．
点评 本题考查抛物线与x轴的交点，解题的关键是能将原抛物线的解析式写成两点式．
练习册系列答案
相关题目
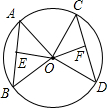如图，在⊙O中，AB、CD是两条弦，OE⊥AB，OF⊥CD，垂足分别为E、F．
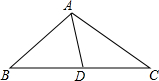如图，AD是△ABC的中线，∠BAD＞∠DAC．求证：AC＞AB．
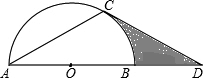如图，点D在⊙O的直径AB的延长线上，过点D作⊙O的切线，切点为C．∠ACD=120°．若⊙O的半径为2，则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π．
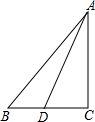如图，在△ABC中，AD=15，AC=12，DC=9，点B是CD延长线上一点，连接AB，若AB=20．求：△ABD的面积．
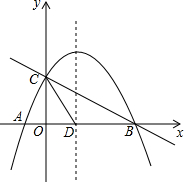如图，直线y1=-$\frac{1}{2}$x+2与x轴，y轴分别交于B，C，抛物线y=ax2+bx+c（a≠0）经过点A，B，C，点A坐标为（-1，0）．