题目内容
15.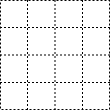 如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.
如图是由16个边长为1的小正方形组成的格点图形,任意连接这些小正方形的若干个顶点,可以得到一些线段,试在图中分别画出两条有理数的线段和两条长度为无理数的线段,并说明理由.
分析 根据有理数的定义画出线段即可.根据勾股定理和无理数的定义画出符合条件的线段即可.
解答 解:如图所示:理由如下:
AB=2,EF=1,2和1都是有理数,
∴AB和EF的长是有理数;
∵AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,QH=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,
$\sqrt{2}$和2$\sqrt{2}$都是无理数,
∴线段AC和线段QH的长是无理数.
点评 本题考查了无理数、有理数和勾股定理的应用,注意:在直角三角形中,两直角边的平方和等于斜边的平方.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.如图,正确画出△ABC中边AC上高的是( )
| A. |  | B. |  | C. |  | D. |  |
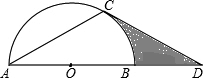 如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
如图,点D在⊙O的直径AB的延长线上,过点D作⊙O的切线,切点为C.∠ACD=120°.若⊙O的半径为2,则图中阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π. 图中曲线是反比例函数y=$\frac{n+7}{x}$的图象的一支.
图中曲线是反比例函数y=$\frac{n+7}{x}$的图象的一支.