题目内容
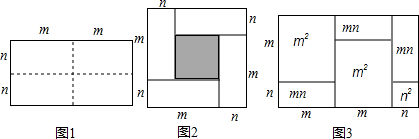
19.沿图1中的虚线将原长方形平均分成四块小长方形,然后按图2的形状拼成一个正方形.(1)图2中阴影部分的正方形的边长可表示为(m-n)2;
(2)观察图2请你写出代数式(m+n)2、(m-n)2、mn之间的等量关系式(m+n)2-(m-n)2=4mn;
(3)根据你得到的关系式解答下列问题:若x+y=-7,xy=5,求(x-y)2的值;
(4)实际上有许多代数恒等式可以用图形的面积来表示,如图3,它表示了(2m+n)(m+n)=2m2+3mn+n2,试画出一个几何图形,使它的面积能表示(m+n)(m+3n)=m2+4mn+3n2.
分析 (1)可直接用正方形的面积公式得到;
(2)掌握完全平方公式,并掌握和与差的区别;
(3)结合完全平方公式进而将原式变形求出即可;
(4)可参照图3进而画出符合题意的图形.
解答 解:(1)阴影部分的边长为(m-n),阴影部分的面积为(m-n)2;
故答案为:(m-n)2;
(2)由题意可得:(m+n)2-(m-n)2=4mn;
故答案为:(m+n)2-(m-n)2=4mn;
(3)∵x+y=-7,xy=5,
∴(x-y)2=(x+y)2-4xy=(-7)2-20=29;
(4)答案不唯一:
它的面积为:m2+4mn+3n2. .
.
点评 本题考查了因式分解的应用,解题关键是认真观察题中给出的图示,用不同的形式去表示面积,熟练掌握完全平方公式,并能进行变形.

练习册系列答案
相关题目
10.我国第六次人口普查显示,全国人口为1370000000人,用科学记数法表示数字1370000000为( )
| A. | 13.7×108 | B. | 1.37×109 | C. | 1.37×108 | D. | 0.137×1010 |
 如图所示的是某个几何体的三视图.
如图所示的是某个几何体的三视图. 如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80. 如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.
如图某超市举行“翻牌”抽奖活动,在一张木板上共有6个相同的牌,其分别对应价值为2元、5元、8元、10元、20元和50元的奖品.
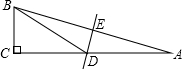 如图,Rt△ACB中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连接BD.若AD=14,则BC的长为( )
如图,Rt△ACB中,∠ACB=90°,∠A=15°,AB的垂直平分线与AC交于点D,与AB交于点E,连接BD.若AD=14,则BC的长为( )