题目内容
9.解方程:(1)2(x-1)+1=0
(2)4(2x-1)-3(5x+1)=14
(3)$5-\frac{x+1}{5}=x$
(4)$\frac{x+1}{2}-\frac{2-3x}{3}=1$.
分析 (1)去括号,移项,合并同类项,将x系数化为1,即可求出解;
(2)去括号,移项,合并同类项,将x系数化为1,即可求出解;
(3)去分母,移项,合并同类项,将x系数化为1,即可求出解;
(2)去分母,移项,合并同类项,将x系数化为1,即可求出解.
解答 解:(1)2(x-1)+1=0
去括号得:2x-2+1=0,
移项、合并同类项得:2x=1,
系数化为1得:x=$\frac{1}{2}$;
(2)4(2x-1)-3(5x+1)=14
去括号得:8x-4-15x-3=14
移项、合并同类项得:-7x=21,
系数化为1得:x=-3;
(3)5-$\frac{x+1}{5}$=x
去分母得:25-x-1=5x
移项、合并同类项得:6x=24,
系数化为1得:x=4;
(4)$\frac{x+1}{2}$-$\frac{2-3x}{3}$=1
去分母得:3x+3-4+6x=6,
移项、合并同类项得:9x=7,
系数化为1得:x=$\frac{7}{9}$.
点评 此题考查了解一元一次方程的解法;其步骤为:去分母,去括号,移项,合并同类项,将未知数系数化为1,求出解.

练习册系列答案
相关题目
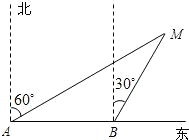 某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里.
某渔船上的渔民在A处观测到灯塔M在北偏东60°方向处,这艘渔船以每小时40海里的速度向正东方向航行,1小时后到达B处,在B处观测到灯塔M在北偏东30°方向处.则B处与灯塔的距离BM是40海里.