题目内容
13.关于x的一元二次方程x2-3x-k=0有两个不相等的实数根.(1)求k的取值范围;
(2)请选择一个k的负整数值,并求出方程的根;
(3)设x1,x2是方程的两个实根,若2x1+x1x2+2x2=8,求k的值.
分析 (1)因为方程有两个不相等的实数根,得到△>0,由此可求k的取值范围;
(2)在k的取值范围内,取负整数,代入方程,解方程即可;
(3)由根与系数的关系得出x1+x2=3,x1x2=-k,代入2x1+x1x2+2x2=8,得到2×3-k=8,解方程即可求出k的值.
解答 解:(1)∵方程有两个不相等的实数根,
∴(-3)2-4(-k)>0,
即4k>-9,解得k>-$\frac{9}{4}$;
(2)若k是负整数,k只能为-1或-2;
取k=-2,原方程为x2-3x+2=0,
解得,x1=1,x2=2;
(3)∵x1,x2是方程的两个实根,
∴x1+x2=3,x1x2=-k,
∵2x1+x1x2+2x2=8,
∴2(x1+x2)+x1x2=8,即2×3-k=8,
解得k=-2.
点评 本题考查了根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
也考查了一元二次方程的解法以及根与系数的关系.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
4.对二次函数y=x2-2x-3,当y<0时,自变量x的取值范围是( )
| A. | -1<x<3 | B. | x<-1 | C. | x>3 | D. | x<-1或x>3 |
8.Rt△ABC中,∠C=90°,AC=5,BC=12,则这个三角形外接圆的半径为( )
| A. | 2.5 | B. | 6 | C. | 6.5 | D. | 8.5 |
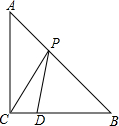 如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5.
如图,在△ABC中,AC=BC=4,∠ACB=90°,D是BC边的一点,且CD=1,P是AB边上一动点,则PC+PD的最小值是5.