题目内容
8.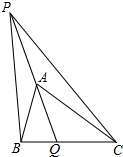 如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.
如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.
分析 根据外角的性质得到∠BAQ=∠CAQ=∠BPC,∠BAQ=∠BPQ+∠ABP,等量代换得到∠ABP=∠APC,同理∠ACP=∠APB,推出△PAB∽△CAP,根据相似三角形的性质得到$\frac{AB}{PA}=\frac{AP}{AC}=\frac{PB}{PC}=\frac{1}{2}$,求得AB=$\frac{1}{2}$ PA,AC=2PA,于是得到$\frac{AB}{AC}$=$\frac{\frac{1}{2}PA}{2PA}$=$\frac{1}{4}$,即可得到结论.
解答 解:∵∠BAQ=∠CAQ=∠BPC,
而∠BAQ=∠BPQ+∠ABP,
∴∠ABP=∠APC,
同理∠ACP=∠APB,
∴△PAB∽△CAP,
$\frac{AB}{PA}=\frac{AP}{AC}=\frac{PB}{PC}=\frac{1}{2}$,
∴AB=$\frac{1}{2}$ PA,
AC=2 PA,
∴$\frac{AB}{AC}$=$\frac{\frac{1}{2}PA}{2PA}$=$\frac{1}{4}$,
在△ABC中,AB:AC=BQ:QC=1:4,
∵BQ=1,
∴CQ=4.
点评 本题考查了相似三角形的判定和性质,角平分线的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.使(x2+px+8)(x2-3x+q)的乘积不含x3和x2,则p、q的值为( )
| A. | p=0,q=0 | B. | p=-3,q=-1 | C. | p=3,q=1 | D. | p=-3,q=1 |
20.计算(-5)+3=( )
| A. | 2 | B. | 8 | C. | 1 | D. | -2 |
 若在象棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点(-1,1).
若在象棋盘上建立直角坐标系,使“将”位于点(1,-2),“象”位于点(3,-2),则“炮”位于点(-1,1). 如图,直线有2条,射线有8条,线段有6条.
如图,直线有2条,射线有8条,线段有6条. 如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交AB于E,交BC于F.BC=6,则BF=2.
如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交AB于E,交BC于F.BC=6,则BF=2. 把正整数1,2,3,…,2015排成如图所示的7列,规定从上到下依次为第1行、第2行、第3行、…,从左到右依次为第1至7列.
把正整数1,2,3,…,2015排成如图所示的7列,规定从上到下依次为第1行、第2行、第3行、…,从左到右依次为第1至7列.