题目内容
3. 如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交AB于E,交BC于F.BC=6,则BF=2.
如图,在△ABC中,AB=AC,∠A=120°,AB的垂直平分线交AB于E,交BC于F.BC=6,则BF=2.
分析 连接AF,根据等腰三角形的性质得到∠B=∠C=30°,根据线段的垂直平分线的性质得到FA=FB,根据直角三角形的性质得到答案.
解答 解: 连接AF,
连接AF,
∵AB=AC,∠A=120°,
∴∠B=∠C=30°,
∵EF是AB的垂直平分线,
∴FA=FB,
∴∠FAB=∠B=30°,
∴∠FAC=90°,又∠C=30°,
∴FA=$\frac{1}{2}$FC,又FA=FB,
∴BF=$\frac{1}{3}$BC=2,
故答案为:2.
点评 本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.

练习册系列答案
相关题目
12.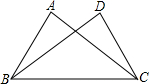 如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
 如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )
如图,△ABC≌△DCB,点A与点D,点B与点C对应,如果AC=6cm,AB=3cm,那么DC的长为( )| A. | 3cm | B. | 5cm | C. | 6cm | D. | 无法确定 |
 如图,在矩形ABCD中,AB=6,BC=2,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是相交.
如图,在矩形ABCD中,AB=6,BC=2,⊙O是以AB为直径的圆,则直线DC与⊙O的位置关系是相交.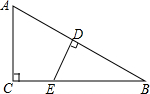 在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.
在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.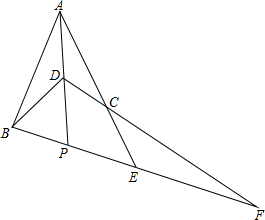 如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.
如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.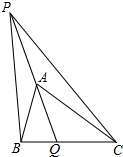 如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.
如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.