题目内容
19.使(x2+px+8)(x2-3x+q)的乘积不含x3和x2,则p、q的值为( )| A. | p=0,q=0 | B. | p=-3,q=-1 | C. | p=3,q=1 | D. | p=-3,q=1 |
分析 根据多项式乘多项式的法则计算,然后根据不含x2项和x3项就是这两项的系数等于0列式,求出p和q的值,从而得出.
解答 解:(x2+px+8)(x2-3x+q),
=x4+(p-3)x3+(8-3p+q)x2+(pq-24)x+8q,
∵(x2+px+8)(x2-3x+q)的展开式中不含x2项和x3项,
∴$\left\{\begin{array}{l}{p-3=0}\\{8-3p+q=0}\end{array}\right.$
解得:$\left\{\begin{array}{l}{p=3}\\{q=1}\end{array}\right.$.
故选:C.
点评 本题考查了多项式乘多项式的运算法则,根据不含哪一项就是让这一项的系数等于0列式是解题的关键.

练习册系列答案
相关题目
9.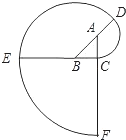 如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )
如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )
 如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )
如图,△ABC是等腰直角三角形,且∠ACB=90°.曲线CDEF…叫做“等腰直角三角形的渐开线”,其中弧CD,弧DE,弧EF,…的圆心依次按A、B、C循环.如果AC=1,那么曲线CDEF的长度为( )| A. | $\frac{12+7\sqrt{2}}{4}π$ | B. | $\frac{7+4\sqrt{2}}{4}π$ | C. | $\frac{5+3\sqrt{2}}{4}π$ | D. | $\frac{10+5\sqrt{2}}{4}$π |
4.一元二次方程x2-2x-1=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 无法确定 |
9.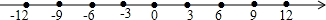 我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
步骤一:实验与操作:
(1)已知点A、B在数轴上分别表示a、b.填写表格
步骤二:观察与猜想:
(2)观察上表:猜想A、B两点之间的距离可以表示为|a-b|(用a、b的代数式表示)
步骤三:理解与应用:
(3)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).
①求两个动点运动的速度;
②A、B两动点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
③若A、B两动点分别从(2)中标出的位置再次同时开始在数轴上运动,运动速度不变,运动方向不限.问:经过几秒后,A、B两动点之间相距4个单位长度.
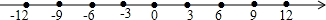 我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!
我们知道:|a|表示数轴上,数a的点到原点的距离.爱动脑筋的小明联系绝对值的概念和“|a|=|a-0|”,进而提出这样的问题:数轴上,数a的点到数1点的距离,是不是可以表示为|a-1|?小明的想法是否正确呢?让我们一起来探究吧!步骤一:实验与操作:
(1)已知点A、B在数轴上分别表示a、b.填写表格
| a | 3 | -5 | 5 | -10 | -5.5 | … |
| b | 7 | 0 | -1 | 2 | -1.5 | … |
| A、B两点之间的距离 | 4 | 5 | … |
(2)观察上表:猜想A、B两点之间的距离可以表示为|a-b|(用a、b的代数式表示)
步骤三:理解与应用:
(3)动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动.运动到3秒时,两点相距15个单位长度.已知动点A、B的速度之比是3:2(速度单位:1个单位长度/秒).
①求两个动点运动的速度;
②A、B两动点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
③若A、B两动点分别从(2)中标出的位置再次同时开始在数轴上运动,运动速度不变,运动方向不限.问:经过几秒后,A、B两动点之间相距4个单位长度.
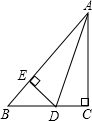 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB,垂足为E.若BC=9,BE=3,则△BDE的周长为( )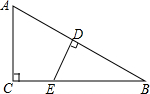 在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.
在Rt△ABC中,∠C=90°,点E在BC上,ED⊥AB于点D,求证:$\frac{AC}{AB}$=$\frac{DE}{BE}$.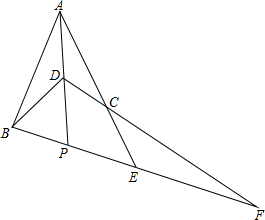 如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.
如图:D在△ABE内部,点C在AE上,AD交BE于P,DC交BE于F,∠ABD=∠ACD,∠PDB=∠PDC.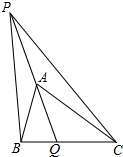 如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.
如图,在△ABC中,AQ是△ABC的角平分线,P是QA延长线上一点.若∠BPC=$\frac{1}{2}$∠BAC,PB:PC=1:2,BQ=1,则CQ的长为4.