题目内容
阅读材料:
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
的近似值.
小明的方法:
∵
<
<
,
设
=3+k(0<k<1).
∴(
)2=(3+k)2.
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈
.
∴
≈3+
≈3.67.
问题:
(1)请你依照小明的方法,估算
的近似值;
(2)请结合上述具体实例,概括出估算
的公式:已知非负整数a、b、m,若a<
<a+1,且m=a2+b,则
≈ (用含a、b的代数式表示);
(3)请用(2)中的结论估算
的近似值为: .
学习了无理数后,某数学兴趣小组开展了一次探究活动:估算
| 13 |
小明的方法:
∵
| 9 |
| 13 |
| 16 |
设
| 13 |
∴(
| 13 |
∴13=9+6k+k2.
∴13≈9+6k.
解得 k≈
| 4 |
| 6 |
∴
| 13 |
| 4 |
| 6 |
问题:
(1)请你依照小明的方法,估算
| 31 |
(2)请结合上述具体实例,概括出估算
| m |
| m |
| m |
(3)请用(2)中的结论估算
| 57 |
考点:估算无理数的大小
专题:阅读型
分析:(1)根据题目信息,找出41前后的两个平方数,从而确定出
=6+k(0<k<1),再根据题目信息近似求解即可;
(2)根据题目提供的求法,先求出k值,然后再加上a即可;
(3)把a换成7,b换成8代入公式进行计算即可得解.
| 31 |
(2)根据题目提供的求法,先求出k值,然后再加上a即可;
(3)把a换成7,b换成8代入公式进行计算即可得解.
解答:解:(1)∵
<
<
,
设
=5+k(0<k<1),
∴(
)2=(5+k)2,
∴31=25+10k+k2,
∴31≈25+10k.
解得k≈
,
∴
≈5+
≈5+0.6=5.6;
(2)设
=a+k(0<k<1),
∴m=a2+2ak+k2≈a2+2ak,
∵m=a2+b,
∴a2+2ak=a2+b,
解得k=
,
∴
≈a+
;
(3)
≈7+
≈7.57.
| 25 |
| 31 |
| 36 |
设
| 31 |
∴(
| 31 |
∴31=25+10k+k2,
∴31≈25+10k.
解得k≈
| 6 |
| 10 |
∴
| 31 |
| 6 |
| 10 |
(2)设
| m |
∴m=a2+2ak+k2≈a2+2ak,
∵m=a2+b,
∴a2+2ak=a2+b,
解得k=
| b |
| 2a |
∴
| m |
| b |
| 2a |
(3)
| 57 |
| 8 |
| 14 |
点评:本题考查了无理数的估算,读懂题目提供信息,然后根据信息中的方法改变数据即可,找出一般性的方法解决问题.

练习册系列答案
相关题目
四个数-3,-2,1,0.5中,相反数最小的是( )
| A、-3 | B、-2 | C、1 | D、0.5 |
 小亮家里装修房子,爸爸想考一考他,爸爸拿出一块四条边都是80cm的瓷砖(瓷砖的平面图如图所示),要求他检验一下四个角是否为直角,能用的工具只有10cm的一段直尺,如果你是小亮,你认为能完成吗?
小亮家里装修房子,爸爸想考一考他,爸爸拿出一块四条边都是80cm的瓷砖(瓷砖的平面图如图所示),要求他检验一下四个角是否为直角,能用的工具只有10cm的一段直尺,如果你是小亮,你认为能完成吗?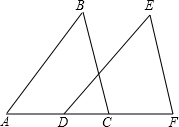 已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.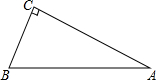 在△ABC中,∠ACB=90°,AC=4,BC=2,以AB为边向外作等腰直角三角形ABD,求CD的长.
在△ABC中,∠ACB=90°,AC=4,BC=2,以AB为边向外作等腰直角三角形ABD,求CD的长.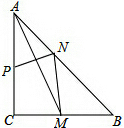 如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为( )
如图,在△ABC中,∠ACB=90°,AC=BC=4,M是CB中点,P、N分别在AC、AB上,若△APN的面积与△ANM的面积相等,则AP长为( )