题目内容
12.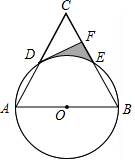 已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
分析 (1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;
(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;
(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE-S扇形DOE进行计算.
解答 (1)证明:连接OD,如图,
∵△ABC为等边三角形,
∴∠A=∠C=60°,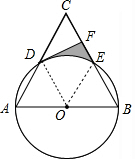
∵OA=OD,
∴∠ODA=∠A=60°,
∴∠ODA=∠C,
∴OD∥BC,
∵DF⊥BC,
∴OD⊥BC,
∴DF为⊙O的切线;
(2)解:∵等边三角形ABC的边长为4,
∴AB=AC=4,∠C=60°,
∵AO=AD=2,
∴CD=2,
在Rt△CDF中,∵sinC=$\frac{DF}{CD}$,
∴DF=2sin60°=$\sqrt{3}$;
(3)解:连接OE,如图,
∵CF=$\frac{1}{2}$CD=1,
∴EF=CE-CF=1,
∴S阴影部分=S梯形ODFE-S扇形DOE=$\frac{1}{2}$(1+2)•$\sqrt{3}$-$\frac{60•π•{2}^{2}}{360}$=$\frac{3\sqrt{3}}{2}$-$\frac{2}{3}$π.
点评 本题考查了切线判定:经过半径的外端且垂直于这条半径的直线是圆的切线.当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了等边三角形的性质和利用割补法计算补规则图形的面积.

练习册系列答案
相关题目
3.某商品现在的售价为每件30元,每天可卖出40件.市场调查反映:如果调整价格,每降价1元,每天可多卖出2件.请你帮助分析,当每件商品降价多少元时,可使每天的销售额最大,最大销售额是多少?设每件商品降价x元,每天的销售额为y元.
(1)分析:根据问题中的数量关系,用含x的式子填表:
(2)由以上分析,用含x的式子表示y,并求出问题的解.
(1)分析:根据问题中的数量关系,用含x的式子填表:
| 原价 | 每件降价1元 | 每件降价2元 | … | 每件降价x元 | |
| 每件售价(元) | 30 | 29 | 28 | … | 30-x |
| 每天销量(件) | 40 | 42 | 44 | … | 40+2x |
1.把根号外的因式化到根号内:-a$\sqrt{-a}$=( )
| A. | $\sqrt{-{a}^{2}}$ | B. | $\sqrt{-{a}^{3}}$ | C. | -$\sqrt{-{a}^{3}}$ | D. | $\sqrt{{a}^{3}}$ |
2.下列变形错误的是( )
| A. | 若-$\frac{1}{2}$x=6,则x=-12 | B. | 若3x=x+1,则2x=1 | ||
| C. | 若x2=y2,则x=y | D. | 若x=y,则x2=y2 |
 已知:如图,AC、BD相交于点O,且AB=DC,AC=DB,则∠A与∠D相等吗?为什么?
已知:如图,AC、BD相交于点O,且AB=DC,AC=DB,则∠A与∠D相等吗?为什么?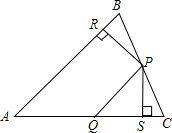 如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.上述结论中正确的是①②.(填序号)
如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:①AS=AR;②QP∥AR;③△BRP≌△CSP.上述结论中正确的是①②.(填序号)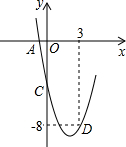 二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).
二次函数y=ax2+bx+c的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).