题目内容
已知△ABC中，∠C=90°，∠A=23°，AB=10．求：
（1）∠B；
（2）AC；
（3）BC．（其中sin23°=0.3907，cos23°=0.9205，tan23°=0.4245）
（1）∠B；
（2）AC；
（3）BC．（其中sin23°=0.3907，cos23°=0.9205，tan23°=0.4245）
考点：解直角三角形
专题：
分析：（1）根据∠B=90°-∠A代入计算即可；
（2）根据cos∠A=
，得出AC=cos∠A•AB，代入计算即可；
（3）根据sin∠A=
，得出BC=sin∠A•AB，代入计算即可．
（2）根据cos∠A=
| AC |
| AB |
（3）根据sin∠A=
| BC |
| AB |
解答：解：（1）∵△ABC中，∠C=90°，∠A=23°，
∴∠B=90°-23°=63°；
（2）∵cos∠A=
，
∴AC=cos∠A•AB=cos23°•10=0.9205×10=9.205；
（3）∵sin∠A=
，
∴BC=sin∠A•AB=sin23°×10=0.3907×10=3.907．
∴∠B=90°-23°=63°；
（2）∵cos∠A=
| AC |
| AB |
∴AC=cos∠A•AB=cos23°•10=0.9205×10=9.205；
（3）∵sin∠A=
| BC |
| AB |
∴BC=sin∠A•AB=sin23°×10=0.3907×10=3.907．
点评：本题考查了解直角三角形，关键是熟练掌握好边角之间的关系，列出算式，求出边角．
练习册系列答案
百年学典课时学练测系列答案
仁爱英语同步练习册系列答案
相关题目
如图，在梯形AOBC中，AO∥CB，点A、B分别在y轴和x轴上．P是OB中点，以P为圆心，PB长为半径作半圆，D为该半圆与AC的一个公共点，且OB=CB=CD=4．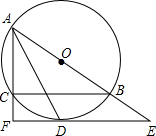
如图，⊙O是△ABC的外接圆，AB为直径，∠BAC的平分线交⊙O于点D，过点D作EF∥BC，EF与AB、AC的延长线分别交于点E、F．
如图，在△ABC中，∠BCA=90°，以BC为直径的⊙O交AB于点P，Q是AC的中点．