题目内容
(1)如图1,已知△ABC中,∠B>∠C,AD⊥BC于D,AE平分∠BAC;
①若∠B=80°,∠C=40°,则∠DAE= 度.
②试用含∠B、∠C的关系式表示∠DAE,则∠DAE= .
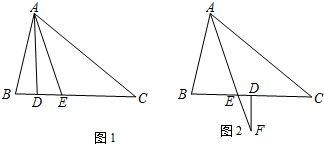
(2)在图2中其它条件不变,若把“AD⊥BC于D”改为“F是AE延长线上的任意一点,FD⊥BC于D”,则∠DFE与∠B、∠C有何关系?试说明理由.
①若∠B=80°,∠C=40°,则∠DAE=
②试用含∠B、∠C的关系式表示∠DAE,则∠DAE=

(2)在图2中其它条件不变,若把“AD⊥BC于D”改为“F是AE延长线上的任意一点,FD⊥BC于D”,则∠DFE与∠B、∠C有何关系?试说明理由.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)依据三角形内角和定理可求得∠BAC的度数,在Rt△ADC中,可求得∠DAC的度数,AE是角平分线,由∠EAC=
∠BAC,故∠EAD=∠EAB-∠DAB;
(2)依据三角形内角和定理,以及角的平方线的性质即可求得.
| 1 |
| 2 |
(2)依据三角形内角和定理,以及角的平方线的性质即可求得.
解答:解:(1)①∵在△ABC中,AE是∠BAC的平分线,且∠B=80°,∠C=40°,
∴∠BAE=∠EAC=
(180°-∠B-∠C)=
(180°-80°-40°)=30°.
在△ABD中,∠ADB=90°,∠B=80°,
∴∠DAB=90°-80°=10°,
∠EAD=∠EAB-∠DAB=30°-10°=20°.
②∠DAE=
(180°-∠B-∠C)-(90°-∠B)=
(∠B-∠C)
故答案是:20,
(∠B-∠C).
(2)∠DFE=
(∠B-∠C)
理由:∠DFE=90°-∠DEF=90°-∠AEB=90°-(
∠A+∠C)=90°-[
(180°-∠B-∠C)+∠C]
=90°-90°+
∠B-
∠C=
(∠B-∠C).
∴∠BAE=∠EAC=
| 1 |
| 2 |
| 1 |
| 2 |
在△ABD中,∠ADB=90°,∠B=80°,
∴∠DAB=90°-80°=10°,
∠EAD=∠EAB-∠DAB=30°-10°=20°.
②∠DAE=
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:20,
| 1 |
| 2 |
(2)∠DFE=
| 1 |
| 2 |
理由:∠DFE=90°-∠DEF=90°-∠AEB=90°-(
| 1 |
| 2 |
| 1 |
| 2 |
=90°-90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了三角形内角和定理、三角形的角平分线、中线和高.求角的度数时,经常用到隐含在题中的“三角形内角和是180°”这一条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F.
如图,线段BC切⊙O于点C,以AC为直径,连接AB交⊙O于点D,点E是BC的中点,交AB于点D,连结OB、DE交于点F. 如图,点E是
如图,点E是