题目内容
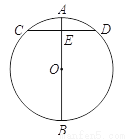
在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.
练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
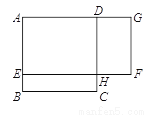
如图,点E是矩形ABCD边AB上一动点(不与点B重合),过点E作EF⊥DE交BC于点F,连接DF.已知AB = 4cm,AD = 2cm,设A,E两点间的距离为xcm,△DEF面积为ycm2.小明根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
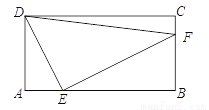
下面是小明的探究过程,请补充完整:
(1)确定自变量x的取值范围是 ;
(2)通过取点、画图、测量、分析,得到了x与y的几组值,如下表:
x/cm | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y/cm2 | 4.0 | 3.7 | 3.9 | 3.8 | 3.3 | 2.0 | … |
(说明:补全表格时相关数值保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(4)结合画出的函数图象,解决问题:当△DEF面积最大时,AE的长度为 cm.
(1);(2)3.8,4.0;(3)画图见解析;(4)0或2. 【解析】试题分析:(1)根据点E是边AB上一动点(不与点B重合)即可得; (2)由题意可得△ADE∽△BEF,由相似三角形对应边成比例可以得到用x表示的BF,由y=S矩形ABCD -S△ADE-S△BEF-S△DCF 根据表格中的数据进行计算即可得; (3)根据表格中的数据进行描点,然后用平滑的曲线连接即可得; ...已知抛物线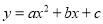 上部分点的横坐标x与纵坐标y的对应值如下表:
上部分点的横坐标x与纵坐标y的对应值如下表:
x | … |
| 0 | 1 | 2 | 3 | … |
y | … | 3 | 0 |
| m | 3 | … |
有以下几个结论:
①抛物线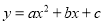 的开口向下;②抛物线
的开口向下;②抛物线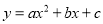 的对称轴为直线
的对称轴为直线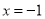 ;③方程
;③方程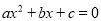 的根为0和2;④当y>0时,x的取值范围是x<0或x>2.其中正确的是( )
的根为0和2;④当y>0时,x的取值范围是x<0或x>2.其中正确的是( )
A. ①④ B. ②④ C. ②③ D. ③④
D 【解析】∵x=-1、3时的值相等, ∴x=0、2时的值相等,y=0,对称轴是直线x=1,故②错误; ∴方程的根为0和2,故③正确; 把(0,0)、(-1,3)、(1,-1)分别代入抛物线的解析式得: , 解得: ,∴解析式为:y=x2-2x, ∴抛物线开口向上,故①错误; 当y>0时,x的取值范围是x<0或x>2,故④正确, 故选D.

 ,
, 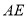 是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:(1)__________________________;(2)______________________.
是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:(1)__________________________;(2)______________________.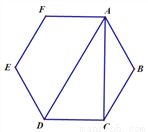
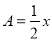 ,
, 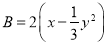 ,
, 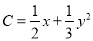 .
.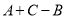 所得的结果;(用含
所得的结果;(用含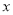 ,
, 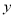 的式子表示)
的式子表示)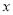 ,
, 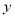 满足
满足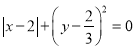 ,求(1)中所得结果的值.
,求(1)中所得结果的值.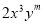 与
与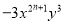 是同类项,则
是同类项,则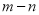 的值是( )
的值是( )
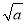 的平方根是±3,则
的平方根是±3,则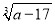 =__________.
=__________.