��Ŀ����
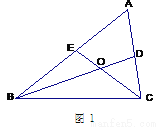
��1����ͼ1���ڡ�ABC�С�A��60 º��BD��CE��Ϊ��ABC�Ľ�ƽ�������ཻ�ڵ�O.
����գ���BOC�� �ȣ�
����֤��BC��BE+CD��(д����֤����)
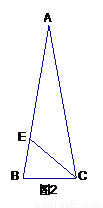
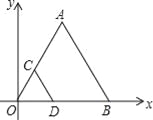
��2����ͼ2���ڡ�ABC�У�AB=AC=m��BC=n�� CEƽ�֡�ACB��
������ABC�����ΪS�����߶�CE����һ��M�����߶�AC����һ��N��ʹ��AM+MN��ֵ��С����AM+MN����Сֵ������ ����������(ֱ��д����)����
������A=20�㣬���BCE���ܳ�������������������(ֱ��д����)��
��ϰ��ϵ�д�
 �����ҵ���������ϵ�д�
�����ҵ���������ϵ�д�
�����Ŀ

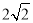 B.
B. 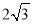 C.
C. 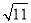 D.
D. 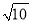
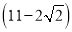 �� B.
�� B. 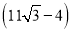 �� C.
�� C. 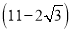 �� D.
�� D. 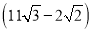 ��
��
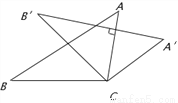
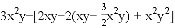 ������
������
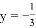 ��
��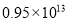 km B.
km B. 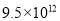 km C.
km C. 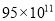 km D.
km D. 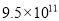 km
km