题目内容
5.一个三角形的三边长分别为$\sqrt{48}$cm、$\sqrt{12}$cm、$\sqrt{27}$cm,则它的周长是9$\sqrt{3}$cm.分析 根据三角形的周长公式可以求得三角形的周长.
解答 解:∵一个三角形的三边长分别为$\sqrt{48}$cm、$\sqrt{12}$cm、$\sqrt{27}$cm,
∴这个三角形的周长是:
$\sqrt{48}+\sqrt{12}+\sqrt{27}$
=4$\sqrt{3}+2\sqrt{3}+3\sqrt{3}$
=9$\sqrt{3}$,
故答案为:9$\sqrt{3}$.
点评 本题考查二次根式的应用,解答本题的关键是明确二次根式的化简,利用三角形的周长公式计算.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
13.实数-$\sqrt{4}$,0,-π,$\sqrt{10}$,0.1010010001…(相邻两个1之间依次多一个0),$\frac{22}{7}$,其中无理数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
10.下列说法正确的是( )
| A. | 同位角相等 | |
| B. | 如果$\sqrt{a}$平方根等于±3,那么a=9 | |
| C. | 过一点有且只有一条直线与已知直线垂直 | |
| D. | 算术平方根等于它本身的数是0和1 |
17.若函数y=(a+3)x+b-2的图象与x轴交于正半轴,与y轴交于负半轴,则( )
| A. | a>-3,b>2 | B. | a<-3,b<2 | C. | a>-3,b<2 | D. | a<-3,b>2 |
 已知二次函数y=-x2+2x+m的部分图象如图,则关于x的一元二次方程-x2+2x+m=3的解为x=0或x=2.
已知二次函数y=-x2+2x+m的部分图象如图,则关于x的一元二次方程-x2+2x+m=3的解为x=0或x=2.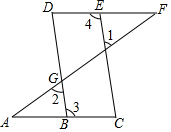 如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.
如图,点E在线段DF上,点B在线段AC上,若∠1=∠2,3=∠4,则∠A=∠F.请将下面证明过程或理由补充完整.