题目内容
已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m-n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+5值等于 .
考点:因式分解的应用
专题:
分析:先将x=2m+n+2和x=m+2n时,多项式x2+4x+5的值相等理解为x=2m+n+2和x=m+2n时,二次函数y=x2+4x+5的值相等,则抛物线的对称轴为直线x=
,又二次函数y=x2+4x+5的对称轴为直线x=-2,得出
=-2,化简得m+n=-2,即可求出当x=3(m+n+1)=3(-2+1)=-3时,x2+4x+5的值.
| 3m+3n+2 |
| 2 |
| 3m+3n+2 |
| 2 |
解答:
解:∵x=2m+n+2和x=m+2n时,多项式x2+4x+5的值相等,
∴二次函数y=x2+4x+5的对称轴为直线x=
,
又∵二次函数y=x2+4x+5的对称轴为直线x=-2,
∴
=-2,
∴3m+3n+2=-4,m+n=-2,
∴当x=3(m+n+1)=3(-2+1)=-3时,
x2+4x+5=(-3)2+4×(-3)+5=2.
故答案为:2.
∴二次函数y=x2+4x+5的对称轴为直线x=
| 3m+3n+2 |
| 2 |
又∵二次函数y=x2+4x+5的对称轴为直线x=-2,
∴
| 3m+3n+2 |
| 2 |
∴3m+3n+2=-4,m+n=-2,
∴当x=3(m+n+1)=3(-2+1)=-3时,
x2+4x+5=(-3)2+4×(-3)+5=2.
故答案为:2.
点评:本题考查了二次函数的性质及多项式求值,难度中等.将x=2m+n+2和x=m+2n时,多项式x2+4x+5的值相等理解为x=2m+n+2和x=m+2n时,二次函数y=x2+4x+5的值相等是解题的关键.

练习册系列答案
相关题目
下列运算正确的是( )
| A、a4+a5=a9 |
| B、2a4×3a5=6a9 |
| C、a3•a3•a3=3a3 |
| D、(-a3)4=a7 |
下列计算正确的是( )
| A、7a+a=7a2 |
| B、5y-3y=2 |
| C、3x2y-2x2y=x2y |
| D、3a+2b=5ab |
某人从A地步行到B地,当走到预定时间时,离B地还有0.5千米;若把步行速度提高25%,则可比预定时间早半小时到达B地.已知AB两地相距12.5千米,则某人原来步行的速度是( )
| A、2千米/时 |
| B、4千米/时 |
| C、5千米/时 |
| D、6千米/时 |
下列条件不能判定四边形ABCD是平行四边形的是( )
| A、AB∥CD,AD∥BC |
| B、AD=BC,AB=CD |
| C、AB∥CD,AD=BC |
| D、∠A=∠C,∠B=∠D |
 如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D,E,AD与CE交于点H.
如图,在△ABC中,AD⊥BC,CE⊥AB,垂足分别为点D,E,AD与CE交于点H.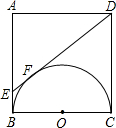 如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为
如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB于点E,则△ADE和直角梯形EBCD的周长之比为