题目内容
如图，夜晚路灯下，小明在点D处测得自己影长DE=4m，在点G处测得自己影长DG=3m，E、D、G、B在同一条直线上，已知小明身高为1.6m，求灯杆AB的高度．考点：相似三角形的应用
专题：计算题
分析：先证明△ECD∽△EAB，利用相似比得到
=
，即
=
，再证明△DFG∽△DAB，利用相似比得到
=
，即
=
，于是得到
=
，可解得BG=9，然后利用
=
求AB的长．
| CD |
| AB |
| ED |
| EB |
| 1.6 |
| AB |
| 4 |
| 4+3+BG |
| FG |
| AB |
| DG |
| DB |
| 1.6 |
| AB |
| 3 |
| 3+BG |
| 4 |
| 4+3+BG |
| 3 |
| 3+BG |
| 1.6 |
| AB |
| 3 |
| 3+9 |
解答：解：∵CD∥AB，
∴△ECD∽△EAB，
∴
=
，即
=
，
∵FG∥AB，
∴△DFG∽△DAB，
∴
=
，即
=
，
∴
=
，解得BG=9，
∴
=
，
∴AB=6.4（m），
即灯杆AB的高度为6.4m．
∴△ECD∽△EAB，
∴
| CD |
| AB |
| ED |
| EB |
| 1.6 |
| AB |
| 4 |
| 4+3+BG |
∵FG∥AB，
∴△DFG∽△DAB，
∴
| FG |
| AB |
| DG |
| DB |
| 1.6 |
| AB |
| 3 |
| 3+BG |
∴
| 4 |
| 4+3+BG |
| 3 |
| 3+BG |
∴
| 1.6 |
| AB |
| 3 |
| 3+9 |
∴AB=6.4（m），
即灯杆AB的高度为6.4m．
点评：本题考查了相似三角形的应用：利用影长测量物体的高度；利用相似测量河的宽度（测量距离）；借助标杆或直尺测量物体的高度．
练习册系列答案
阅读快车系列答案
相关题目
如图，在梯形ABCD中，AD∥BC，AB⊥AD，BD⊥CD，如果AD=1，BC=3，那么BD长是
已知：如图在数轴上有A，B两点，它们分别对应着-12和8．A、B两点同时出发，B点以每秒2个单位的速度向右运动，A点则已每秒4个单位的速度向右运动．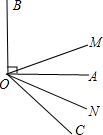
如图，已知∠AOB是直角，ON平分∠AOC，OM平分∠BOC，则∠MON=
如图，∠AOB=90°，OC是∠BOD的平分线，若∠1：∠3=7：9．求∠BOD的度数．