题目内容
 如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.
如图,甲建筑物的高AB为40m,AB⊥BC,DC⊥BC,某数学学习小组开展测量乙建筑物高度的实践活动,从B点测得D点的仰角为60°,从A点测得D点的仰角为45°.求乙建筑物的高DC.考点:解直角三角形的应用-仰角俯角问题
专题:几何图形问题
分析:过点A作AE⊥CD于点E,可得四边形ABCE为矩形,根据∠DAE=45°,可得AE=ED,设AE=DE=xm,则BC=xm,在Rt△BCD中,利用仰角为60°,可得CD=BC•tan60°,列方程求出x的值,继而可求得CD的高度.
解答:解:过点A作AE⊥CD于点E,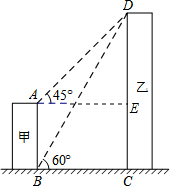
∵AB⊥BC,DC⊥BC,
∴四边形ABCE为矩形,
∴CE=AB=40m,
∵∠DAE=45°,
∴AE=ED,
设AE=DE=xm,则BC=xm,
在Rt△BCD中,
∵∠DBC=60°,
∴CD=BC•tan60°,
即40+x=
x,
解得:x=20(
+1),
则CD的高度为:x+40=60+20
(m).
答:乙建筑物的高DC为(60+20
)m.

∵AB⊥BC,DC⊥BC,
∴四边形ABCE为矩形,
∴CE=AB=40m,
∵∠DAE=45°,
∴AE=ED,
设AE=DE=xm,则BC=xm,
在Rt△BCD中,
∵∠DBC=60°,
∴CD=BC•tan60°,
即40+x=
| 3 |
解得:x=20(
| 3 |
则CD的高度为:x+40=60+20
| 3 |
答:乙建筑物的高DC为(60+20
| 3 |
点评:本题考查了解直角三角形的应用,解答本题的关键是根据仰角和俯角构造直角三角形,利用三角函数的知识解直角三角形,难度一般.

练习册系列答案
相关题目
下列结论中.正确的是( )
| A、若|a|=|b|,则a=b |
| B、若a≠b,则|a|≠|b| |
| C、若a≠b,则|a|=|b| |
| D、若a+b=0,则|a|=|b| |
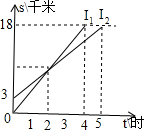 小李家、小于家、学校在同一条路线上,小李和小于分别从家同时出发到学校,如图l1,l2分别表示小李和小于前往学校所走的路程s/千米与所用的时间t/时的关系.
小李家、小于家、学校在同一条路线上,小李和小于分别从家同时出发到学校,如图l1,l2分别表示小李和小于前往学校所走的路程s/千米与所用的时间t/时的关系. 如图,在△ABC中,AB=AC,BC=4cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于
如图,在△ABC中,AB=AC,BC=4cm,AB的垂直平分线交AB于点D,交边AC于点E,△BCE的周长等于18cm,则AC的长等于