题目内容
17. 如图,矩形ABCD中,E是边BC的一点,F是边CD的中点,CE=k•BE,且四边形AECF的面积为2.
如图,矩形ABCD中,E是边BC的一点,F是边CD的中点,CE=k•BE,且四边形AECF的面积为2.(1)当k=1时,求AB•BE的值;
(2)用含k的代数式表示△ABE的面积.
分析 (1)由CE=BE,DF=CF,推出S△AFD=S△AFC,S△AEC=S△AEB,推出四边形ABCD的面积=2•四边形AECF的面积,推出AB•BC=4,由此即可解决问题.
(2)设△AEB的面积为x,则△ACE的面积为kx,△AFC的面积为$\frac{1}{2}$(x+kx),由题意可得kx+$\frac{1}{2}$(x+kx)=2,解方程即可.
解答 解:(1)如图,连接AC.
∵k=1,CE=kBE,
∴CE=BE,∵DF=CF,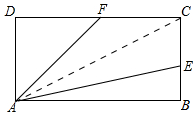
∴S△AFD=S△AFC,S△AEC=S△AEB,
∴四边形ABCD的面积=2•四边形AECF的面积=4,
∴AB×BC=4,
∵BC=2BE,
∴AB•2BE=4,
∴AB•BE=2.
(2)设△AEB的面积为x,则△ACE的面积为kx,△AFC的面积为$\frac{1}{2}$(x+kx),
由题意kx+$\frac{1}{2}$(x+kx)=2,解得x=$\frac{4}{3k+1}$,
∴△ABE的面积为$\frac{4}{3k+1}$.
点评 本题考查矩形的性质、三角形的面积.三角形的中线的性质等知识,解题的关键是学会添加常用辅助线,学会构建方程解决问题,属于中考常考题型.

练习册系列答案
相关题目
7.如图①,在平行四边形ABCD中,∠B=120°,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为xcm,△PAB的面积为ycm2,y关于x的函数的图象如图②所示,则图②中F点的横坐标为( )
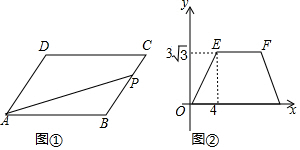

| A. | 7 | B. | 8 | C. | 4+2$\sqrt{3}$ | D. | 4+$\sqrt{3}$ |