题目内容
8．已知a、b、c分别是△ABC的三边，其中a=1，c=4，且关于x的方程$\frac{1}{2}$x2-bx+3b-4=0有两个相等的实数根，试判断△ABC的形状．分析 由方程的系数结合根的判别式即可得出△=b2-6b+8=0，解之即可得出b值，再根据三角形的三边关系即可确定b值，根据a、b、c间的关系即可得出三角形ABC为等腰三角形．
解答 解：∵方程有两个相等的实数根，
∴△=b2-6b+8=0，
解得：b1=2，b2=4，
∵a、b、c是三角形的三边，
∴3＜b＜5，
∴b1=2舍去，
∴b=4=c．
∴三角形ABC为等腰三角形．
点评 本题考查了根的判别式、三角形三边关系以及等腰三角形的判定，根据根的判别式结合三角形三边关系找出b=c是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
18．
如图，直线AB，CD，EF相交于点O，则∠COF的一个邻补角是（ ）
如图，直线AB，CD，EF相交于点O，则∠COF的一个邻补角是（ ）| A． | ∠BOF | B． | ∠DOF | C． | ∠AOE | D． | ∠DOE |
有理数a，b在数轴上的对应位置如图所示，则下列说法正确的有①④（填序号）．
16．△ABC三个顶点的坐标分别为A（2，2），B（4，2），C（6，6），在此直角坐标系中作△DEF，使得△DEF与△ABC位似，且以原点O为位似中心，位似比为1：2，则△DEF的面积为（ ）
| A． | $\frac{1}{2}$ | B． | 1 | C． | 2 | D． | 4 |
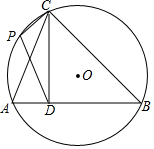△ABC内接于圆O，CD⊥AB于D，CD=DB=3，AD=1，点P为$\widehat{AC}$上一点，求$\frac{\sqrt{10}}{2}$DP+CP的最小值．
13．下列四个图形中，对称轴最多的图形是（ ）
| A． |  | B． |  | C． |  | D． |  |
如图，矩形ABCD中，E是边BC的一点，F是边CD的中点，CE=k•BE，且四边形AECF的面积为2．