题目内容
如图甲,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E,设BD=m,CE=n
(1)求DE的长(用含m,n的代数式表示);
(2)如图乙,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a(0°<a<180°),设BD=m,CE=n.问DE的长如何表示?并请证明你的结论.

(1)求DE的长(用含m,n的代数式表示);
(2)如图乙,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a(0°<a<180°),设BD=m,CE=n.问DE的长如何表示?并请证明你的结论.

考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:(1)由条件可证明△ADB≌△CEA,可得到AE=BD,AD=CE,从而可表示出DE;
(2)方法同(1)证明△ADB≌△CEA,可得到AE=BD,AD=CE,从而可表示出DE.
(2)方法同(1)证明△ADB≌△CEA,可得到AE=BD,AD=CE,从而可表示出DE.
解答:解:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ADB和△CEA中
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=m+n;
(2)DE=m+n,证明如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠DBA=∠CAE,
在△ADB和△CEA中
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=m+n.
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD
在△ADB和△CEA中
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=m+n;
(2)DE=m+n,证明如下:
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°-α,
∴∠DBA=∠CAE,
在△ADB和△CEA中
|
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE=m+n.
点评:本题主要考查全等三角形的判定和性质,掌握三角形全等的判定方法SSS、SAS、ASA、AAS和HL是解题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
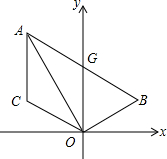 如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.
如图,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴与G,连OB、OC.