题目内容
9.我们把a、b、c三个数中最大的一个数记为D(a,b,c),直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有且只有两个交点,则m的取值为m=$\frac{3}{2}$、m=$\sqrt{2}$或0<m<1.分析 画出函数图象,找出直线与函数D(-x2+1,x-1,-x-1)的图象有一个、两个、三个交点的临界点,再结合图形即可得出结论.
解答 解:画出函数图象,如图所示.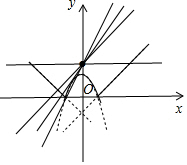
当直线y=mx+$\frac{3}{2}$与y=x-1平行,即m=1时,
直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象只有一个交点;
当直线y=mx+$\frac{3}{2}$与x轴平行,即m=0时,
直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有两个交点;
当直线y=mx+$\frac{3}{2}$过点(-1,0)时,有-m+$\frac{3}{2}$=0,即m=$\frac{3}{2}$,
此时直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象只有一个交点;
当直线y=mx+$\frac{3}{2}$与y=-x2+1相切时,方程x2+mx+$\frac{1}{2}$=0有两个相等的实数根,
∴△=m2-4×1×$\frac{1}{2}$=0,m=$\sqrt{2}$,
此时直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有两个交点.
综上所述:当m=$\frac{3}{2}$、m=$\sqrt{2}$或0<m<1时,直线y=mx+$\frac{3}{2}$(m>0)与函数D(-x2+1,x-1,-x-1)的图象有且只有两个交点.
故答案为:m=$\frac{3}{2}$、m=$\sqrt{2}$或0<m<1.
点评 本题考查了一次函数的性质、二次函数的性质以及数形结合,画出函数图象,利用数形结合是解题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.如图所示,100个小圆形纸片按如图方式粘贴在一条直线上,相邻两个圆重叠部分最宽处是d(单位cm),若d是圆的直径的四分之一,则纸带的总长度AB为( )


| A. | 400d cm | B. | 300d cm | C. | 304d cm | D. | 301d cm |
4.文具店、书店和玩具店依次坐落在一条东西走向的大街上,文具店在书店西边20米处,玩具店位于书店东边100米处,小明从书店沿街向东走了40米,接着又向东走了-60米,此时小明的位置在( )
| A. | 文具店 | B. | 玩具店 | C. | 文具店西40米处 | D. | 玩具店西60米处 |
14.二次函数y=-2(x-3)2+1的图象的顶点坐标是( )
| A. | (3,1) | B. | (3,-1) | C. | (-3,1) | D. | (-3,-1) |
1.用配方法解一元二次方程 x2+6x+6=0,则方程可变形为( )
| A. | (x-3)2=3 | B. | (x+3)2=3 | C. | (x-6)2=30 | D. | (x+6)2=30 |
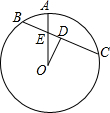 如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.
如图,D是⊙O弦BC的中点,A是⊙O上的一点,OA与BC交于点E,已知AO=8,BC=12.