题目内容
12.已知整数a,b满足($\frac{2}{9}$)a•($\frac{3}{4}$)b=8,则a-b=1.分析 根据($\frac{2}{9}$)a•($\frac{3}{4}$)b=8可得2a-2b×3-2a+b=23,从而知a-2b=3、-2a+b=0,两式相减后即可得.
解答 解:∵($\frac{2}{9}$)a•($\frac{3}{4}$)b=2a•3-2a•3b•2-2b=2a-2b×3-2a+b=23,
∴$\left\{\begin{array}{l}{a-2b=3}&{①}\\{-2a+b=0}&{②}\end{array}\right.$,
①-②,得:3a-3b=3,
∴a-b=1,
故答案为:1.
点评 本题主要考查同底数幂的乘法及负整数指数幂,熟练掌握同底数幂的乘法及负整数指数幂的法则和定义是解题的关键.

练习册系列答案
相关题目
9.在-|-2|,0,(-1)2016,-4这四个数中,最大的数是( )
| A. | -4 | B. | -|-2| | C. | 0 | D. | (-1)2016 |
1.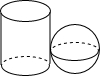 如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
 如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )
如图,圆柱和球在同一水平面上紧靠在一起组成一个几何体,茗茗画出了它的三视图,其中所画的俯视图应该是( )| A. | 两个外离的圆 | B. | 两个相交的圆 | C. | 两个外切的圆 | D. | 两个内切的圆 |
 如图,要使四边形木架不变形,至少要钉上1根木条.
如图,要使四边形木架不变形,至少要钉上1根木条.