题目内容
5.【探究证明】(1)某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究,提出下列问题,请你给出证明.
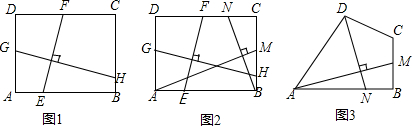
如图1,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H.求证:$\frac{EF}{GH}$=$\frac{AD}{AB}$;
【结论应用】
(2)如图2,在满足(1)的条件下,又AM⊥BN,点M,N分别在边BC,CD上,若$\frac{EF}{GH}$=$\frac{11}{15}$,则$\frac{BN}{AM}$的值为$\frac{11}{15}$;
【联系拓展】
(3)如图3,四边形ABCD中,∠ABC=90°,AB=AD=10,BC=CD=5,AM⊥DN,点M,N分别在边BC,AB上,求$\frac{DN}{AM}$的值.
分析 (1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,易证AP=EF,GH=BQ,△PDA∽△QAB,然后运用相似三角形的性质就可解决问题;
(2)只需运用(1)中的结论,就可得到$\frac{EF}{GH}$=$\frac{AD}{AB}$=$\frac{BN}{AM}$,就可解决问题;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,易证四边形ABSR是矩形,由(1)中的结论可得$\frac{DN}{AM}$=$\frac{AR}{AB}$.设SC=x,DS=y,则AR=BS=5+x,RD=10-y,在Rt△CSD中根据勾股定理可得x2+y2=25①,在Rt△ARD中根据勾股定理可得(5+x)2+(10-y)2=100②,解①②就可求出x,即可得到AR,问题得以解决.
解答 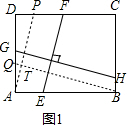 解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
解:(1)过点A作AP∥EF,交CD于P,过点B作BQ∥GH,交AD于Q,如图1,
∵四边形ABCD是矩形,∴AB∥DC,AD∥BC.
∴四边形AEFP、四边形BHGQ都是平行四边形,
∴AP=EF,GH=BQ.
又∵GH⊥EF,∴AP⊥BQ,
∴∠QAT+∠AQT=90°.
∵四边形ABCD是矩形,∴∠DAB=∠D=90°,
∴∠DAP+∠DPA=90°,
∴∠AQT=∠DPA.
∴△PDA∽△QAB,
∴$\frac{AP}{BQ}$=$\frac{AD}{AB}$,
∴$\frac{EF}{GH}$=$\frac{AD}{AB}$;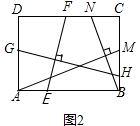
(2)如图2,
∵EF⊥GH,AM⊥BN,
∴由(1)中的结论可得$\frac{EF}{GH}$=$\frac{AD}{AB}$,$\frac{BN}{AM}$=$\frac{AD}{AB}$,
∴$\frac{BN}{AM}$=$\frac{EF}{GH}$=$\frac{11}{15}$.
故答案为$\frac{11}{15}$;
(3)过点D作平行于AB的直线,交过点A平行于BC的直线于R,交BC的延长线于S,如图3,
则四边形ABSR是平行四边形.
∵∠ABC=90°,∴?ABSR是矩形,
∴∠R=∠S=90°,RS=AB=10,AR=BS.
∵AM⊥DN,
∴由(1)中的结论可得$\frac{DN}{AM}$=$\frac{AR}{AB}$.
设SC=x,DS=y,则AR=BS=5+x,RD=10-y,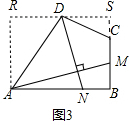
∴在Rt△CSD中,x2+y2=25①,
在Rt△ARD中,(5+x)2+(10-y)2=100②,
由②-①得x=2y-5③,
解方程组$\left\{\begin{array}{l}{{x}^{2}+{y}^{2}=25}\\{x=2y-5}\end{array}\right.$,得
$\left\{\begin{array}{l}{x=-5}\\{y=0}\end{array}\right.$(舍去),或$\left\{\begin{array}{l}{x=3}\\{y=4}\end{array}\right.$,
∴AR=5+x=8,
∴$\frac{DN}{AM}$=$\frac{AR}{AB}$=$\frac{8}{10}$=$\frac{4}{5}$.
点评 本题主要考查了矩形的判定与性质、相似三角形的判定与性质、勾股定理、解二元二次方程组等知识,运用(1)中的结论是解决第(2)、(3)小题的关键.

| A. | -x3+3x3=2x3 | B. | x+x=x2 | C. | x3+2x5=3x3 | D. | x5-x4=x |
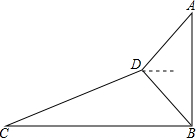 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)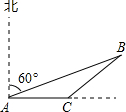 三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
三国魏人刘徽,自撰《海岛算经》,专论测高望远.某校王老师根据《海岛算经》中的问题,编了这样一道题:如图,甲、乙两船同时由港口A出发开往海岛B,甲船沿北偏东60°方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,在C港口停留0.5小时后再沿东北方向开往B岛,其速度仍为20海里/小时.B岛建有一座灯塔,在灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔,两船看到灯塔的时间相差多少?(精确到分钟,$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)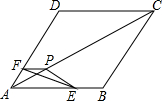 如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$.
如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6$\sqrt{3}$,∠BAD=60°,且AB>6$\sqrt{3}$. 古希腊人常用小石子在沙滩上摆成各种形状来研究数.称图中的数1,5,12,22…为五边形数,则第6个五边形数是51.
古希腊人常用小石子在沙滩上摆成各种形状来研究数.称图中的数1,5,12,22…为五边形数,则第6个五边形数是51. 已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3
已知二次函数y=ax2-2ax+c(a>0)的图象与x轴的负半轴和正半轴分别交于A、B两点,与y轴交于点C,它的顶点为P,直线CP与过点B且垂直于x轴的直线交于点D,且CP:PD=2:3