��Ŀ����
12����һ��ʵ����$\sqrt{9}$��$\sqrt{2}$��$\frac{2}{3}$��1+�У�-$\frac{7}{3}$��-����1�������Ƿ��࣬������Ӧ�������ڣ�
������{$\sqrt{9}$��$\frac{2}{3}$��-$\frac{7}{3}$��}��
������{$\sqrt{2}$��1+��-��}��
��2������ѡ��2����������2�������������á�+��-�������¡��е�3�ֲ�ͬ��������Ž�ѡ����4�����������㣨���������ţ���ʹ������Ľ����һ����������
���� ��1�����ķ�����ʵ�ʲ�����ʽ���������Ȼ����ٷ��ࣻ
��2������Ŀ�𰸲�Ψһ������Ҫ������Ľ����һ��������������������ֻ��ȡ1+�С�-�У�ע����ĿҪ��
��� �⣺��1����Ϊ$\sqrt{9}=3$�������������У�$\sqrt{9}$��$\frac{2}{3}$��-$\frac{7}{3}$���������У�$\sqrt{2}$��1+�У�-�У�
�ʣ�������{ $\sqrt{9}$��$\frac{2}{3}$��-$\frac{7}{3}$ ��}��
������{$\sqrt{2}$��1+��-��}��
��2���𰸲�Ψһ�������������ǣ�$\frac{2}{3}$��-$\frac{7}{3}$�������������ǣ�1+�У�-�У�
[1+��+��-��]��[$\frac{2}{3}$-��-$\frac{7}{3}$��]
=1��3=3��
���� ���⿼����ʵ���ķ����Լ�ʵ���Ļ�����㣮ʵ���ķ��ࣺʵ��$\left\{\begin{array}{l}{������\left\{\begin{array}{l}{����\left\{\begin{array}{l}{������}\\{0}\\{������}\end{array}\right.}\\{����\left\{\begin{array}{l}{������}\\{������}\end{array}\right.}\end{array}\right.}\\{������}\end{array}\right.$

 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�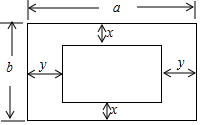 ��ͼ�����������ı������ƣ��Ҷ�Ӧ����ƽ�У������н�����ȷ���ǣ�������
��ͼ�����������ı������ƣ��Ҷ�Ӧ����ƽ�У������н�����ȷ���ǣ�������| A�� | $\frac{y}{x}$=1 | B�� | $\frac{y}{x}$=$\frac{a}{b}$ | C�� | $\frac{y}{x}$=$\frac{b}{a}$ | D�� | ���Ͼ�����ȷ |
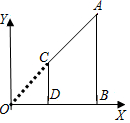 ��ͼ��AB��CD����ֱ��x�ᣬ����ֱ�ΪB��D����A��6��3����C��2��1����
��ͼ��AB��CD����ֱ��x�ᣬ����ֱ�ΪB��D����A��6��3����C��2��1�������OCD���ı���ABDC�������Ϊ��������
| A�� | 1��2 | B�� | 1��3 | C�� | 1��4 | D�� | 1��8 |
| A�� |  | B�� |  | C�� |  | D�� |  |
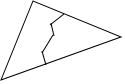 С����С�Ĵ�����һ�鲣������ͼ�����������ϰ����Ϳ����Ӱ�������»���һ����ԭ���IJ�����ȫ��ͬ�IJ�����������ǣ�������
С����С�Ĵ�����һ�鲣������ͼ�����������ϰ����Ϳ����Ӱ�������»���һ����ԭ���IJ�����ȫ��ͬ�IJ�����������ǣ�������| A�� | SAS | B�� | SSS | C�� | ASA | D�� | AAS |
| A�� | ��1��3�� | B�� | ��3��1�� | C�� | ��2��1�� | D�� | ��3��2�� |